DiffEqFlux.jl – Julia 神经微分方程库

2019 年 1 月 18 日 | Chris Rackauckas, Mike Innes, Yingbo Ma, Jesse Bettencourt, Lyndon White, Vaibhav Dixit

翻译：繁体中文

在本博文中，我们将向您展示如何在 Julia 中轻松、高效且稳健地将微分方程 (DiffEq) 求解器与神经网络一起使用。

Flux ODE Training Animation

《神经常微分方程》论文甚至在获得 2018 年 NeurIPS 最佳论文之一之前就引起了广泛关注。该论文已经给出了将这两个截然不同的领域结合起来的一些令人振奋的结果，但这仅仅是个开始：神经网络和微分方程天生就是为了在一起。本博文是 Flux、DifferentialEquations.jl 作者以及神经 ODE 论文作者之间的合作，将解释原因，概述这项工作的当前和未来方向，并开始展示最先进工具的可能性。

Julia DifferentialEquations.jl 库在数值求解微分方程方面的优势已在其他文章中详细讨论。除了它对经典 Fortran 方法进行的广泛基准测试，它还包括其他现代功能，例如GPU 加速、分布式（多节点）并行 和复杂的事件处理。最近，这些原生 Julia 微分方程求解器已成功嵌入到 Flux 深度学习包中，以允许在神经网络中使用经过全面测试和优化的 DiffEq 方法套件。使用新的软件包 DiffEqFlux.jl，我们将向读者展示如何使用各种微分方程模型（包括刚性常微分方程、随机微分方程、延迟微分方程和混合（不连续）微分方程）轻松地将微分方程层添加到神经网络中。

这是第一个将功能齐全的微分方程求解器库和神经网络无缝结合在一起的工具箱。本博文还将展示为什么需要完整微分方程求解器套件的灵活性。通过能够将神经网络与 ODE、SDE、DAE、DDE、刚性方程以及用于伴随灵敏度计算的不同方法融合在一起，这是对神经 ODE 工作的重大推广，并将使研究人员能够更好地探索问题域。

（注意：如果您对此项工作感兴趣，并且是本科生或研究生，我们在此领域有Google Summer of Code 项目可用。这在整个夏天支付相当丰厚的报酬。请加入Julia Slack 和 #jsoc 频道以更详细地讨论。）

  1. 微分方程与机器学习有什么关系？
  2. 什么是神经常微分方程 (ODE)？
  3. 如何求解 ODE？
  4. 让我们将 ODE 放入神经网络框架中！
  5. 为什么完整 ODE 求解器套件对于做好这件事是必要的？
  6. 有哪些类型的微分方程？
  7. 在 Julia 中实现神经 ODE 层
  8. 通过示例了解神经 ODE 层的行为
  9. 核心技术挑战：通过微分方程求解器进行反向传播
  10. 结论

微分方程与机器学习有什么关系？

不熟悉该领域的人可能首先问的一个问题是，为什么微分方程在这种情况下很重要？简单的答案是，微分方程是一种通过数学编码先验结构假设来指定任意非线性变换的方法。

让我们稍微分解一下这个陈述。有三种常见的定义非线性变换的方法：直接建模、机器学习和微分方程。直接写下非线性函数只有在你了解输入和输出之间确切的函数形式时才有效。但是，在许多情况下，这种确切的关系并非先验已知。那么，如果你不知道非线性，如何进行非线性建模呢？

解决此问题的一种方法是使用机器学习。在典型的机器学习问题中，你会得到一些输入 xx，并且你想预测一个输出 yy。从 xx 生成预测 yy 是一个机器学习模型（我们称之为 MLML）。在训练期间，我们试图调整 MLML 的参数，使其生成准确的预测。然后，我们可以使用 MLML 进行推理（即，为新输入 xx 生成 yy）。这仅仅是一个非线性变换 y=ML(x)y=ML(x)。之所以 MLML 很有趣，是因为它的形式很简单，但它会适应数据本身。例如，一个简单的带有 sigmoid 激活函数的神经网络（以设计矩阵形式表示）仅仅是矩阵乘法，后面跟着 sigmoid 函数的应用。具体来说，

ML(x)=σ(W3⋅σ(W2⋅σ(W1⋅x)))ML(x)=\sigma(W_{3}\cdot\sigma(W_{2}\cdot\sigma(W_{1}\cdot x)))

这是一个三层深层神经网络，其中 W=(W1,W2,W3)W=(W_1,W_2,W_3) 是可学习的参数。然后选择 WW 使得 ML(x)=yML(x)=y 合理地拟合你想要拟合的函数。机器学习的理论和实践证实，这是一种学习非线性的好方法。例如，通用逼近定理指出，对于足够多的层或足够多的参数（即足够大的 WiW_{i} 矩阵），ML(x)ML(x) 可以近似任何非线性函数足够接近（受常见约束条件限制）。

所以很好，这总是有效！但它有一些注意事项，主要的是它必须从数据中直接学习关于非线性变换的所有内容。在许多情况下，我们不知道完整的非线性方程，但我们可能知道它的结构细节。例如，非线性函数可能是森林中兔子的数量，我们可能知道它们的出生率取决于当前的数量。因此，与其从无到有，我们可能希望利用这种已知的先验关系和一组定义它的参数。对于兔子，假设我们想要学习

rabbits tomorrow=Model(rabbits today).\text{rabbits tomorrow} = \text{Model}(\text{rabbits today}).

在这种情况下，我们事先知道出生率取决于当前的数量。用数学方法说明这种结构假设的方法是通过微分方程。在这里，我们说的是，在给定的时间点，当兔子数量更多时，兔子种群的出生率会增加。最简单的编码方法是

rabbits′(t)=α⋅rabbits(t)\text{rabbits}'(t) = \alpha\cdot \text{rabbits}(t)

其中 α\alpha 是某个可学习常数。如果你懂微积分，这里解是来自起点的指数增长，增长率为 α\alpha：rabbits(tstart)e(αt)\text{rabbits}(t_\text{start})e^{(\alpha t)}. 但是请注意，我们不需要知道微分方程的解来验证这个想法：我们编码了模型的结构，数学本身就会输出解应该是什么。因此，微分方程一直是大多数科学的首选工具。例如，物理定律告诉你电量如何产生力（麦克斯韦方程组）。这些本质上是关于事物如何变化的方程，因此“事物将处于何处”是微分方程的解。但在最近几十年，这种应用已经发展得更远，在系统生物学领域，通过编码已知的生物结构和数学枚举我们的假设，来学习细胞相互作用；或者在系统药理学中，通过 PK/PD 建模，来了解靶向药物剂量。

因此，随着我们的机器学习模型不断发展，对越来越多的数据的需求，微分方程已成为指定非线性函数的诱人选择，这种方式既可学习（通过参数），又受约束。它们本质上是将输入和输出之间结构关系的先验领域特定知识纳入模型的一种方法。从这种看待两种方法的角度来看，两种方法都各有优缺点，使它们成为建模的互补工具。将它们以新颖和令人兴奋的方式结合起来，似乎是科学实践中一个明确的下一步！

什么是神经常微分方程 (ODE)？

神经常微分方程是将这两个领域结合起来的众多方法之一。最简单的解释是，我们希望学习非线性变换的结构，而不是直接学习非线性变换。因此，我们不是做y=ML(x)y=ML(x)，而是将机器学习模型放在导数上，y′(x)=ML(x)y'(x) = ML(x)，然后求解常微分方程。为什么要这样做呢？一个动机是，以这种方式定义模型，然后使用最简单、最容易出错的方法（欧拉方法）求解常微分方程，你得到的结果相当于一个 残差神经网络。欧拉方法的工作原理基于这样一个事实，即y′(x)=dydxy'(x) = \frac{dy}{dx}，因此

Δy=(ynext−yprev)=Δx⋅ML(x)\Delta y = (y_\text{next} - y_\text{prev}) = \Delta x\cdot ML(x)

这意味着

yi+1=yi+Δx⋅ML(xi).y_{i+1} = y_{i} + \Delta x\cdot ML(x_{i}).

这在结构上与 ResNet 类似，ResNet 是最成功的图像处理模型之一。神经常微分方程论文的见解是，越来越深、越来越强大的类似 ResNet 的模型有效地近似了一种“无限深”的模型，因为每层都趋向于零。我们不需要添加更多层，而是可以直接对微分方程进行建模，然后使用专门的常微分方程求解器来求解。数值常微分方程求解器是一门科学，可以追溯到第一台计算机，现代常微分方程求解器可以自适应地选择步长Δx\Delta x，并使用高阶近似来大幅减少所需的实际步数。事实证明，这在实践中也很好用。

如何求解 ODE？

首先，如何以数值方式指定和求解常微分方程？如果你不熟悉常微分方程求解，你可能想观看我们的 Julia 中常微分方程求解视频教程，并查看 DifferentialEquations.jl 文档的常微分方程教程。思路是通过导数方程 u'=f(u,p,t) 定义一个 ODEProblem，并提供一个初始条件 u0 和一个时间跨度 tspan 来进行求解，并指定参数 p。

例如，Lotka-Volterra 方程描述了兔子和狼的种群动态。它们可以写成

x′=αx+βxyx^\prime = \alpha x + \beta x y y′=−δy+γxyy^\prime = -\delta y + \gamma x y

并在 Julia 中进行编码，例如

using DifferentialEquations
function lotka_volterra(du,u,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = α*x - β*x*y
  du[2] = dy = -δ*y + γ*x*y
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)

然后，要解微分方程，只需对 prob 调用 solve

sol = solve(prob)
using Plots
plot(sol)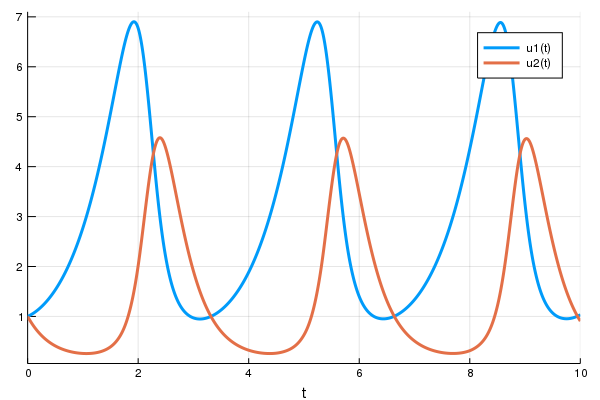

LV Solution Plot

最后要注意的是，我们可以将初始条件 (u0) 和时间跨度 (tspans) 定义为参数 (p 的元素) 的函数。例如，我们可以定义 ODEProblem

u0_f(p,t0) = [p[2],p[4]]
tspan_f(p) = (0.0,10*p[4])
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0_f,tspan_f,p)

在这种形式下，问题的方方面面都由参数向量 (p，在相关文献中称为 θ) 决定。这种方法的实用性将在后面讨论。

DifferentialEquations.jl 提供了许多强大的选项，用于自定义精度、容差、求解器方法、事件等；请查看 文档，详细了解如何在更高级的应用中使用它。

让我们将 ODE 放入神经网络框架中！

为了了解如何将 ODE 嵌入神经网络，让我们看一下神经网络层实际上是什么。层实际上只是一个 *可微函数*，它接受一个大小为 n 的向量，并输出一个大小为 m 的新向量。就是这样！传统上，层是简单的函数，例如矩阵乘法，但在 可微编程 的精神下，人们越来越多地尝试更复杂的函数，例如射线追踪器和物理引擎。

事实证明，微分方程求解器也适合这个框架：求解器接受某个向量 p（可能包括参数，例如初始起点），并输出某个新向量，即解。此外，它是可微的，这意味着我们可以直接将其放入更大的可微程序中。这个更大的程序可以包含神经网络，我们可以继续使用标准优化技术（如 ADAM）来优化它们的权重。

DiffEqFlux.jl 使得进行这种操作变得很方便；让我们试一试。首先，我们将像以前一样解决一个方程，但没有梯度。

p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)
sol = solve(prob,Tsit5(),saveat=0.1)
A = sol[1,:] # length 101 vector

让我们绘制 ODE 解的 (t,A)，看看我们得到了什么

plot(sol)
t = 0:0.1:10.0
scatter!(t,A)

Data points plot

solve 的好处在于它处理了类型处理，使其与神经网络框架（此处为 Flux）兼容。为了说明这一点，让我们定义一个神经网络，其中函数是我们的单个层，然后定义一个损失函数，该函数是输出值与 1 之间的平方距离。在 Flux 中，这看起来像

using Flux, DiffEqFlux
p = [2.2, 1.0, 2.0, 0.4] # Initial Parameter Vector
params = Flux.params(p)

function predict_rd() # Our 1-layer "neural network"
  solve(prob,Tsit5(),p=p,saveat=0.1)[1,:] # override with new parameters
end

loss_rd() = sum(abs2,x-1 for x in predict_rd()) # loss function

现在，我们告诉 Flux 通过运行 100 个 epochs 来训练神经网络，以最小化我们的损失函数 (loss_rd())，从而获得优化后的参数

data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function () #callback function to observe training
  display(loss_rd())
  # using `remake` to re-create our `prob` with current parameters `p`
  display(plot(solve(remake(prob,p=p),Tsit5(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the initial parameter values.
cb()

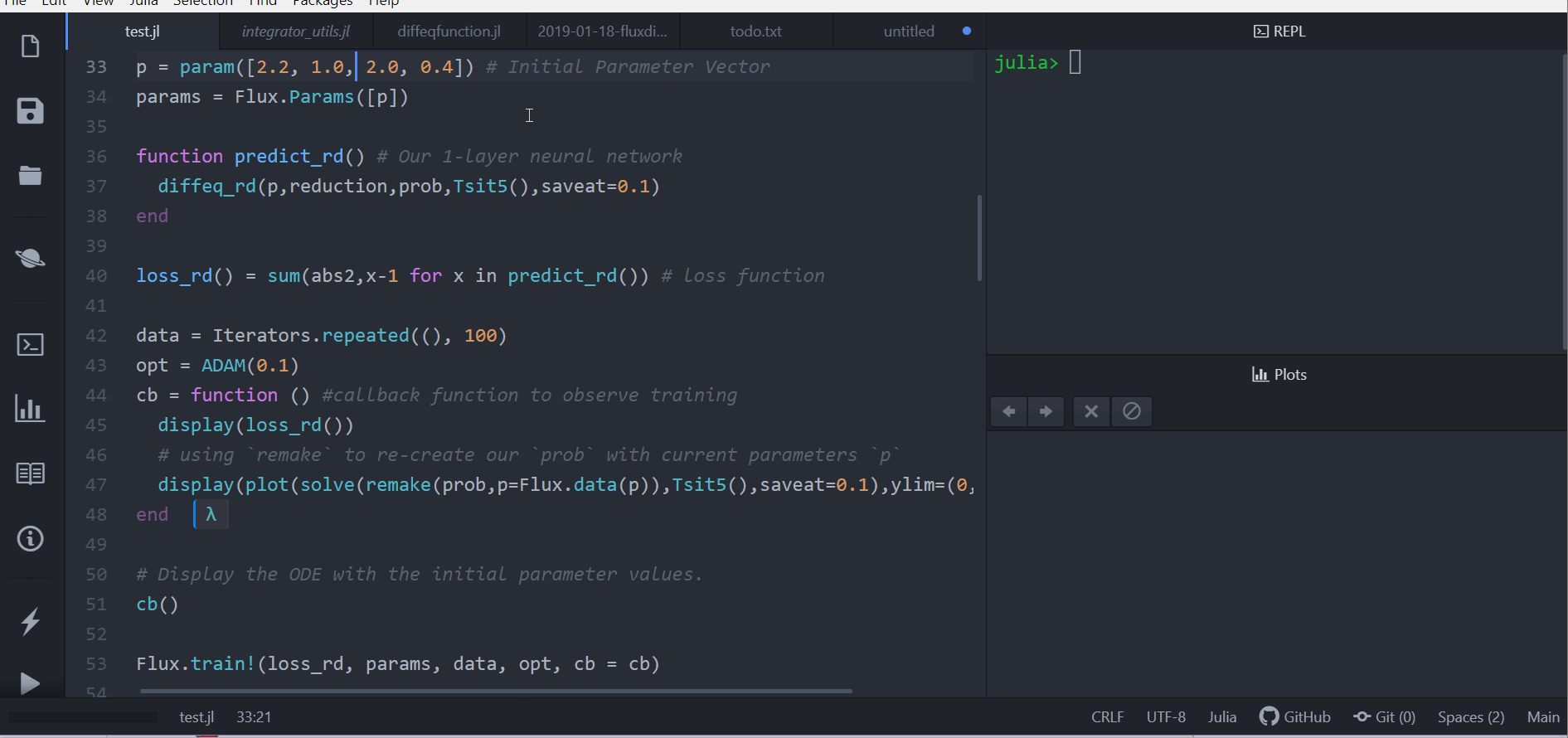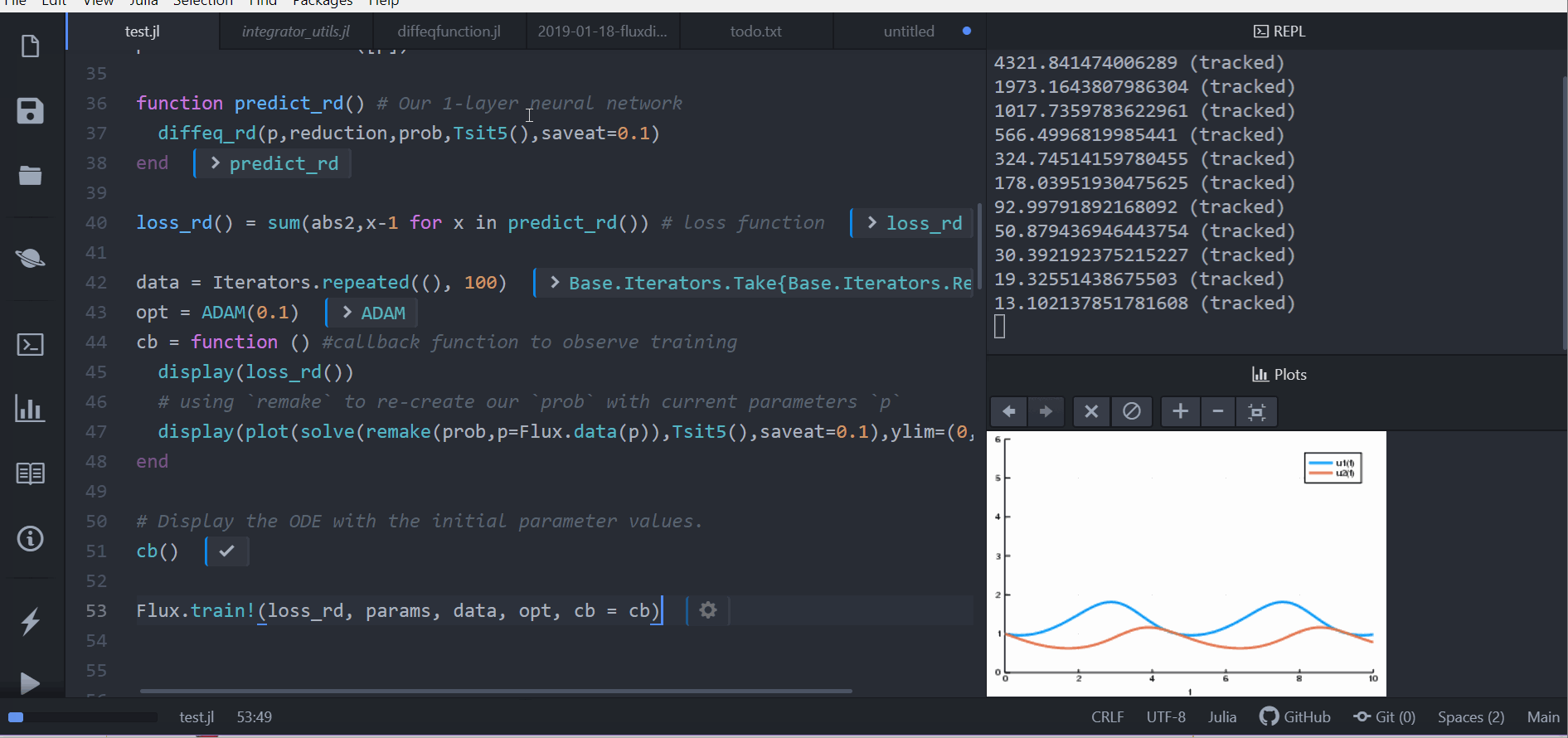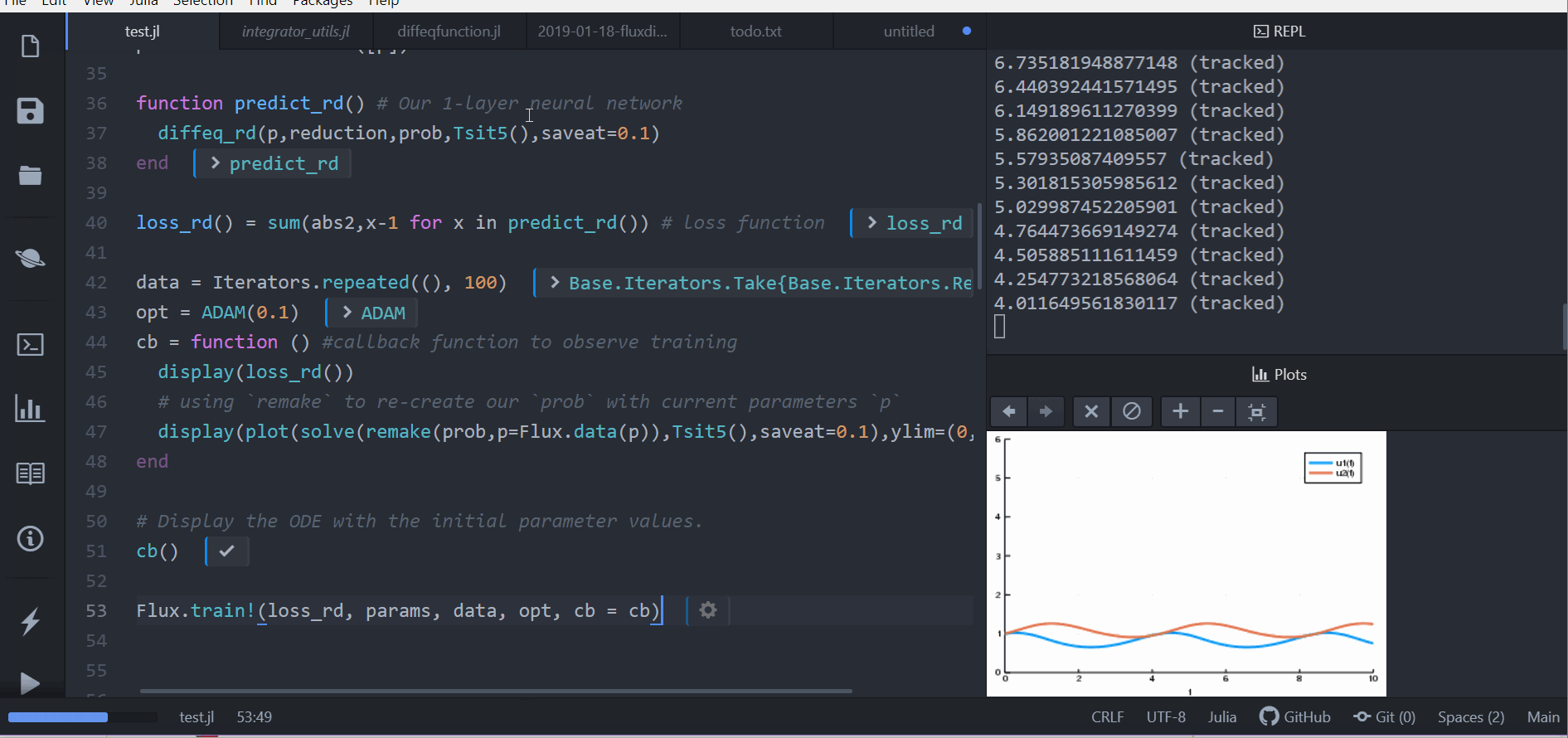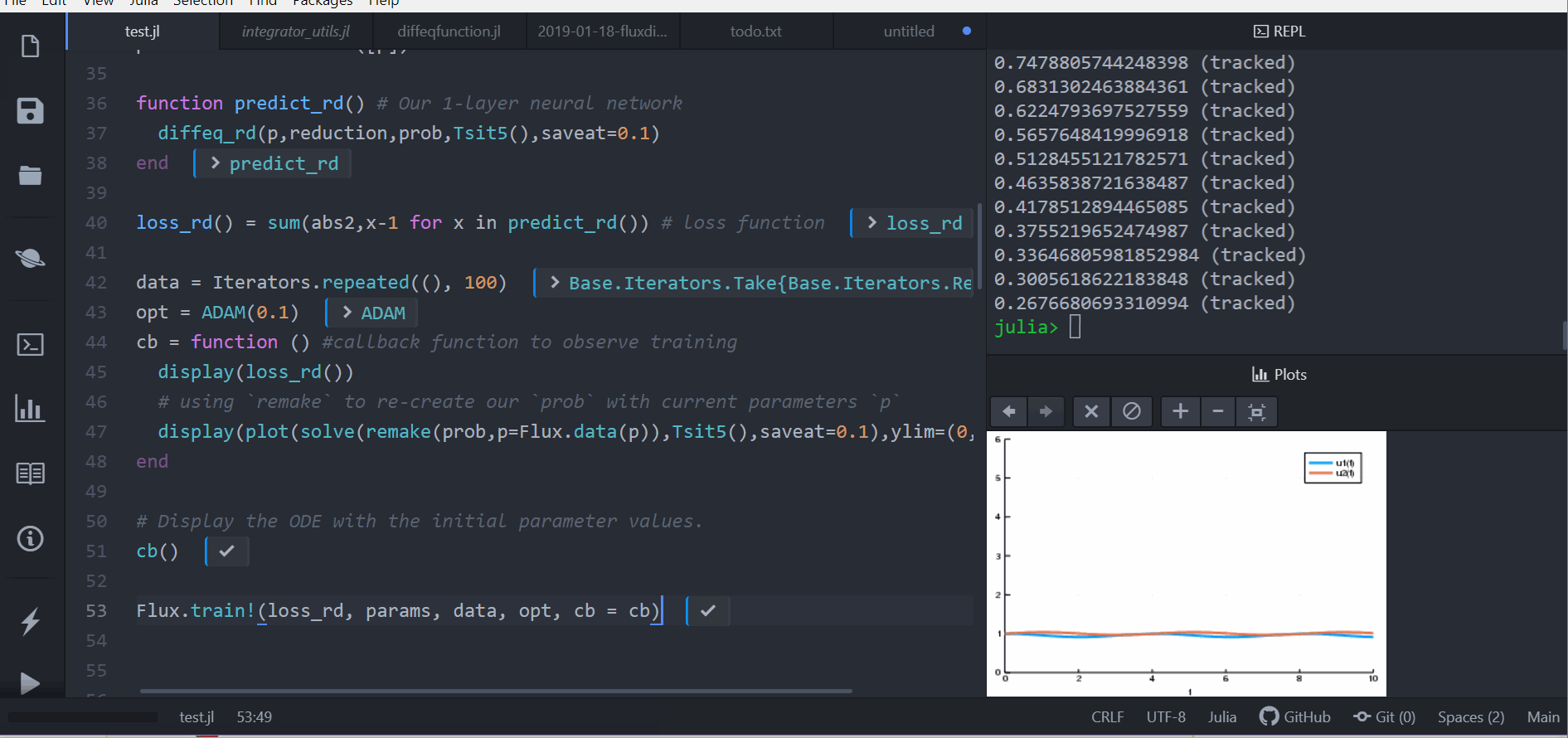
Flux.train!(loss_rd, params, data, opt, cb = cb)

结果是顶部显示的动画。 此代码可在模型库中找到

Flux 找到了使代价函数最小化的神经网络参数 (p)，即它训练了神经网络：碰巧的是，神经网络的前向传递包括求解 ODE。由于我们的代价函数在兔子数量远离 1 时会进行惩罚，因此我们的神经网络找到了参数，使我们的兔子和狼种群都保持在恒定的 1。

现在，我们已经将求解 ODE 作为一层，我们可以在任何地方添加它。例如，多层感知器在 Flux 中的写法是

m = Chain(
  Dense(28^2, 32, relu),
  Dense(32, 10),
  softmax)

如果我们有一个合适的 ODE，它接受适当大小的参数向量，我们可以直接将其放入其中

m = Chain(
  Dense(28^2, 32, relu),
  # this would require an ODE of 32 parameters
  p -> solve(prob,Tsit5(),p=p,saveat=0.1)[1,:],
  Dense(32, 10),
  softmax)

或者我们可以将其放入卷积神经网络中，其中前几层定义了 ODE 的初始条件

m = Chain(
  Conv((2,2), 1=>16, relu),
  x -> maxpool(x, (2,2)),
  Conv((2,2), 16=>8, relu),
  x -> maxpool(x, (2,2)),
  x -> reshape(x, :, size(x, 4)),
  x -> solve(prob,Tsit5(),u0=x,saveat=0.1)[1,:],
  Dense(288, 10), softmax) |> gpu

只要你能写下前向传递，我们就可以取任何参数化的可微程序并对其进行优化。世界是你的牡蛎。

为什么完整 ODE 求解器套件对于做好这件事是必要的？

在将现有的求解器套件和深度学习库结合起来的情况下，出色的 torchdiffeq 项目采取了另一种方法，而是直接在 PyTorch 中实现求解器方法，包括自适应龙格-库塔 4-5 (dopri5) 和亚当斯-巴什福斯-穆尔顿方法 (adams)。但是，虽然他们的方法对某些类型的模型非常有效，但没有访问完整的求解器套件会有限制。

考虑以下示例，即 ROBER ODE。亚当斯-巴什福斯-穆尔顿方法最经过充分测试（和优化）的实现是 C++ 包 SUNDIALS 中的 CVODE 集成器（经典 LSODE 的派生）。让我们使用 DifferentialEquations.jl 来调用 CVODE 及其亚当斯方法，让它为我们求解 ODE

using ParameterizedFunctions # required for the `@ode_def` macro
using Sundials

rober = @ode_def Rober begin
  dy₁ = -k₁*y₁+k₃*y₂*y₃
  dy₂ =  k₁*y₁-k₂*y₂^2-k₃*y₂*y₃
  dy₃ =  k₂*y₂^2
end k₁ k₂ k₃
prob = ODEProblem(rober,[1.0;0.0;0.0],(0.0,1e11),(0.04,3e7,1e4))
solve(prob,CVODE_Adams())

（对于熟悉在 MATLAB 中求解 ODE 的用户来说，这类似于 ode113）

这种方法和 恩斯特·海勒的 Fortran 套件 中的 dopri 方法都会停滞并无法求解方程。这是因为 ODE 是 刚性的，因此“稳定区域较小”的方法将无法适当地求解它（有关更多详细信息，我建议阅读海勒的《常微分方程求解 II》。另一方面，KenCarp4() 对这个问题来说，方程在眨眼间就得到了求解

sol = solve(prob,KenCarp4())
using Plots
plot(sol,xscale=:log10,tspan=(0.1,1e11))

ROBER Plot

这只是一个集成细微之处的例子：通过 PI 自适应控制器稳定显式方法、隐式求解器中的步长预测等，所有这些都是需要大量时间和测试才能变得高效和健壮的复杂细节。不同的问题需要不同的方法： 辛几何积分器 是 充分处理物理许多问题而不会漂移 所必需的，而诸如 IMEX 积分器 等工具是处理 来自偏微分方程 的 ODE 所必需的。因此，构建一个生产级求解器是一项巨大的工程，而且现有的求解器相对较少。

与其在适合科学计算的求解器套件之外并行构建一个特定于 ML 的求解器套件，在 Julia 中，它们是同一个，这意味着你可以立即利用所有这些方法。

有哪些类型的微分方程？

常微分方程只是微分方程的一种。你可以在微分方程的结构中添加许多其他功能。例如，未来兔子的数量并不取决于当前的兔子数量，因为母兔从孩子受孕到怀孕需要一段时间。因此，兔子的出生率实际上是由于过去的兔子数量。在微分方程的导数中使用滞后项会使该方程被称为延迟微分方程 (DDE)。由于 DifferentialEquations.jl 处理 DDE 的方式与处理 ODE 相同，因此它也可以用作 Flux 中的层。以下是一个示例

function delay_lotka_volterra(du,u,h,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = (α - β*y)*h(p,t-0.1)[1]
  du[2] = dy = (δ*x - γ)*y
end
h(p,t) = ones(eltype(p),2)
prob = DDEProblem(delay_lotka_volterra,[1.0,1.0],h,(0.0,10.0),constant_lags=[0.1])

p = [2.2, 1.0, 2.0, 0.4]
params = Flux.params(p)

using SciMLSensitivity
function predict_rd_dde()
  solve(prob,MethodOfSteps(Tsit5()),p=p,sensealg=TrackerAdjoint(),saveat=0.1)[1,:]
end
loss_rd_dde() = sum(abs2,x-1 for x in predict_rd_dde())
loss_rd_dde()

此示例的完整代码（包括生成动画） 可在模型库中找到

此外，我们可以向我们的微分方程添加随机性，以模拟随机事件如何导致额外出生或比预期更多的死亡。这种方程被称为随机微分方程 (SDE)。由于 DifferentialEquations.jl 处理 SDE（并且目前是唯一具有自适应刚性和非刚性 SDE 积分器的库），因此它们可以像 Flux 中的层一样进行处理。以下是一个带有 SDE 的神经网络层

function lotka_volterra_noise(du,u,p,t)
  du[1] = 0.1u[1]
  du[2] = 0.1u[2]
end
prob = SDEProblem(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,5.0))

p = [2.2, 1.0, 2.0, 0.4]
params = Flux.params(p)
function predict_sde()
  solve(prob,SOSRI(),p=p,sensealg=TrackerAdjoint(),saveat=0.1,
                     abstol=1e-1,reltol=1e-1)[1,:]
end
loss_rd_sde() = sum(abs2,x-1 for x in predict_sde())
loss_rd_sde()

我们可以训练神经网络来观察它的运行，并找到使兔子数量接近恒定的参数

data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function ()
  display(loss_rd_sde())
  display(plot(solve(remake(prob,p=p),SOSRI(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the current parameter values.
cb()

Flux.train!(loss_rd_sde, params, data, opt, cb = cb)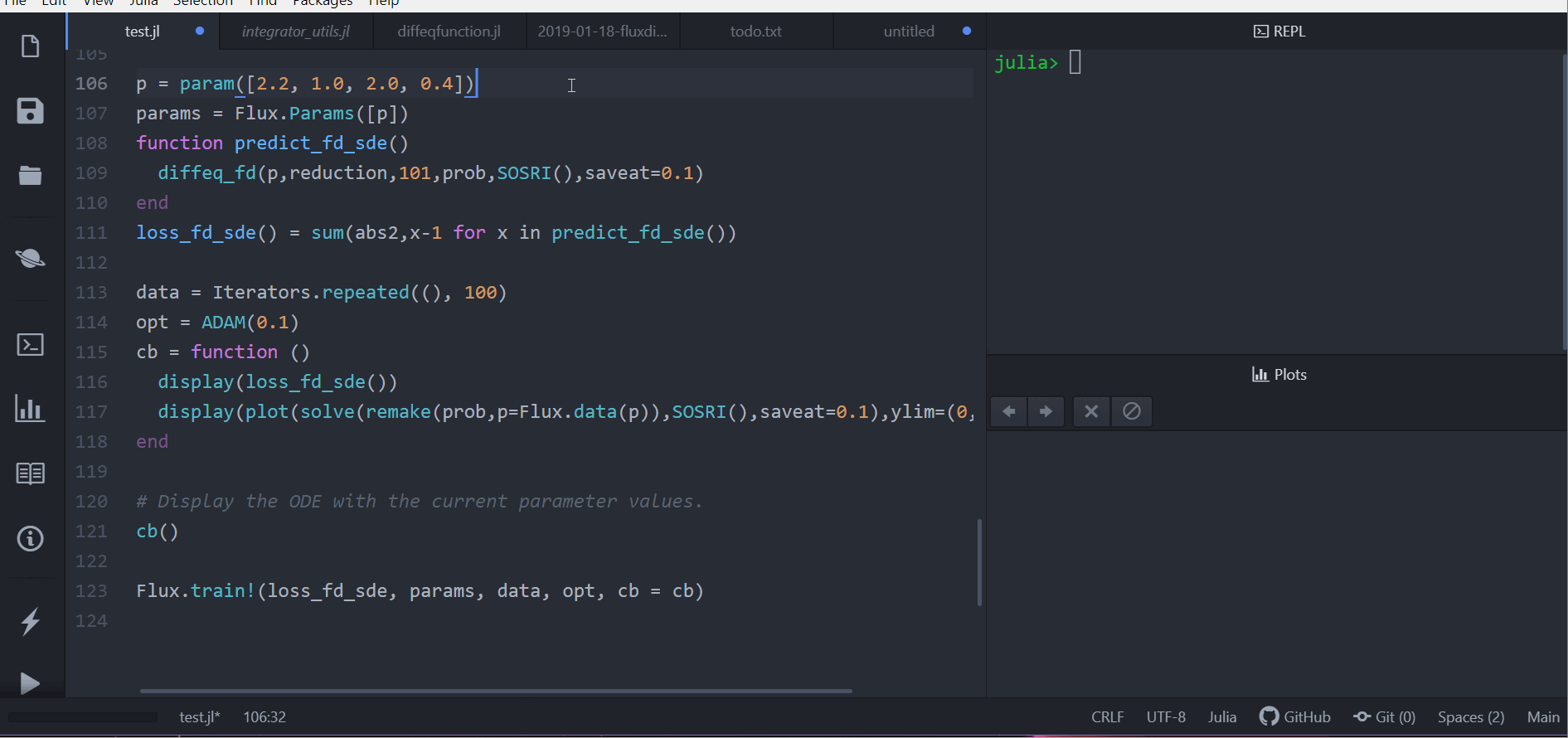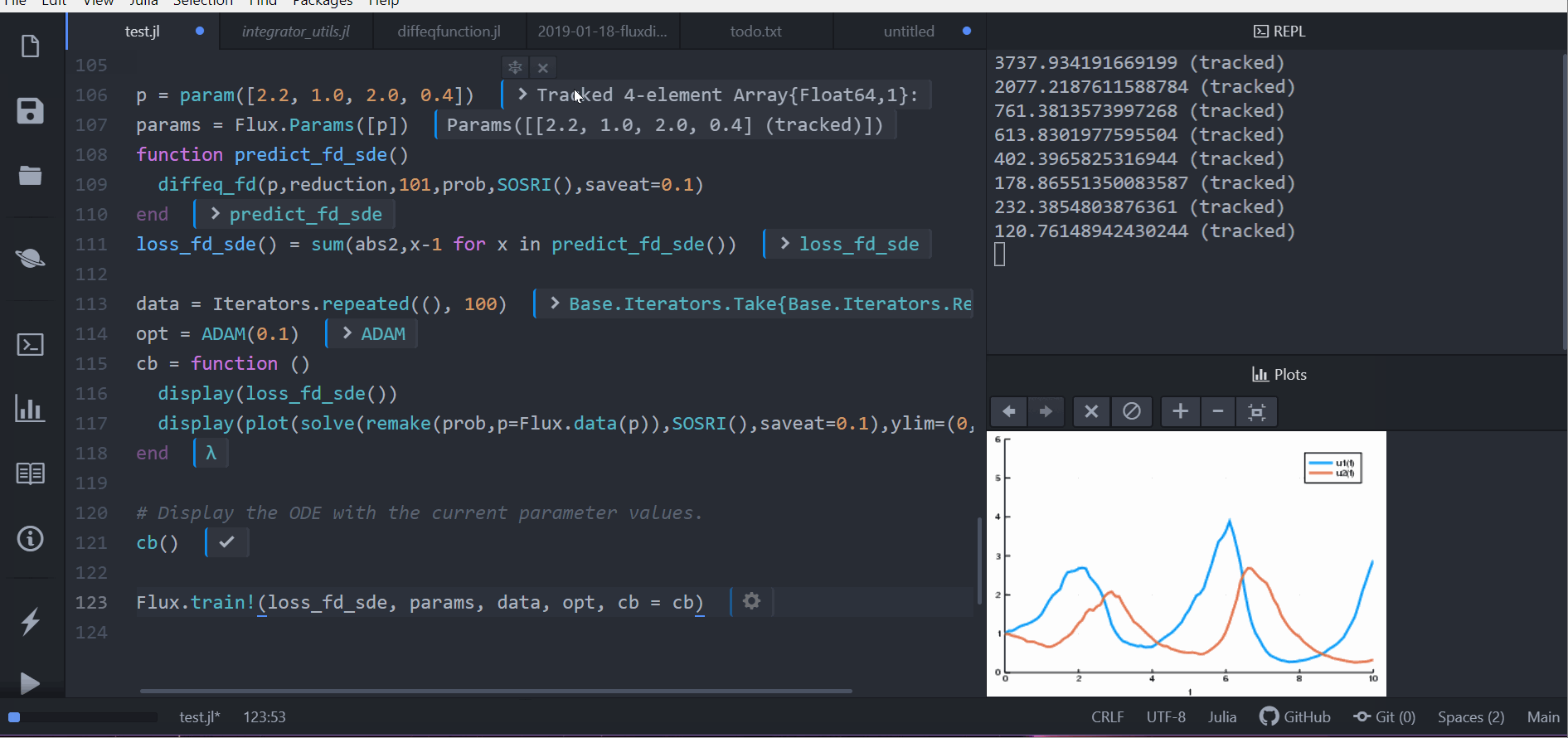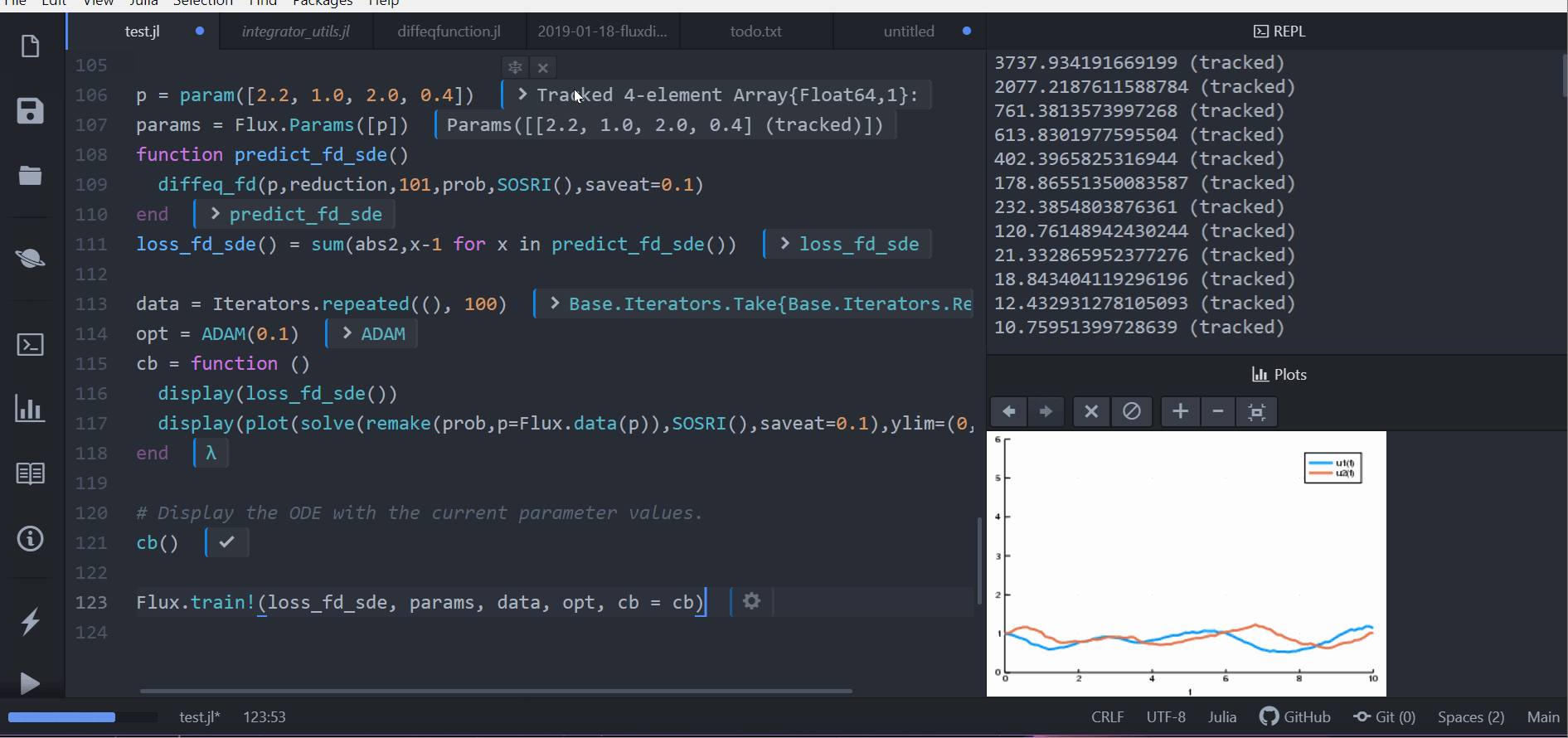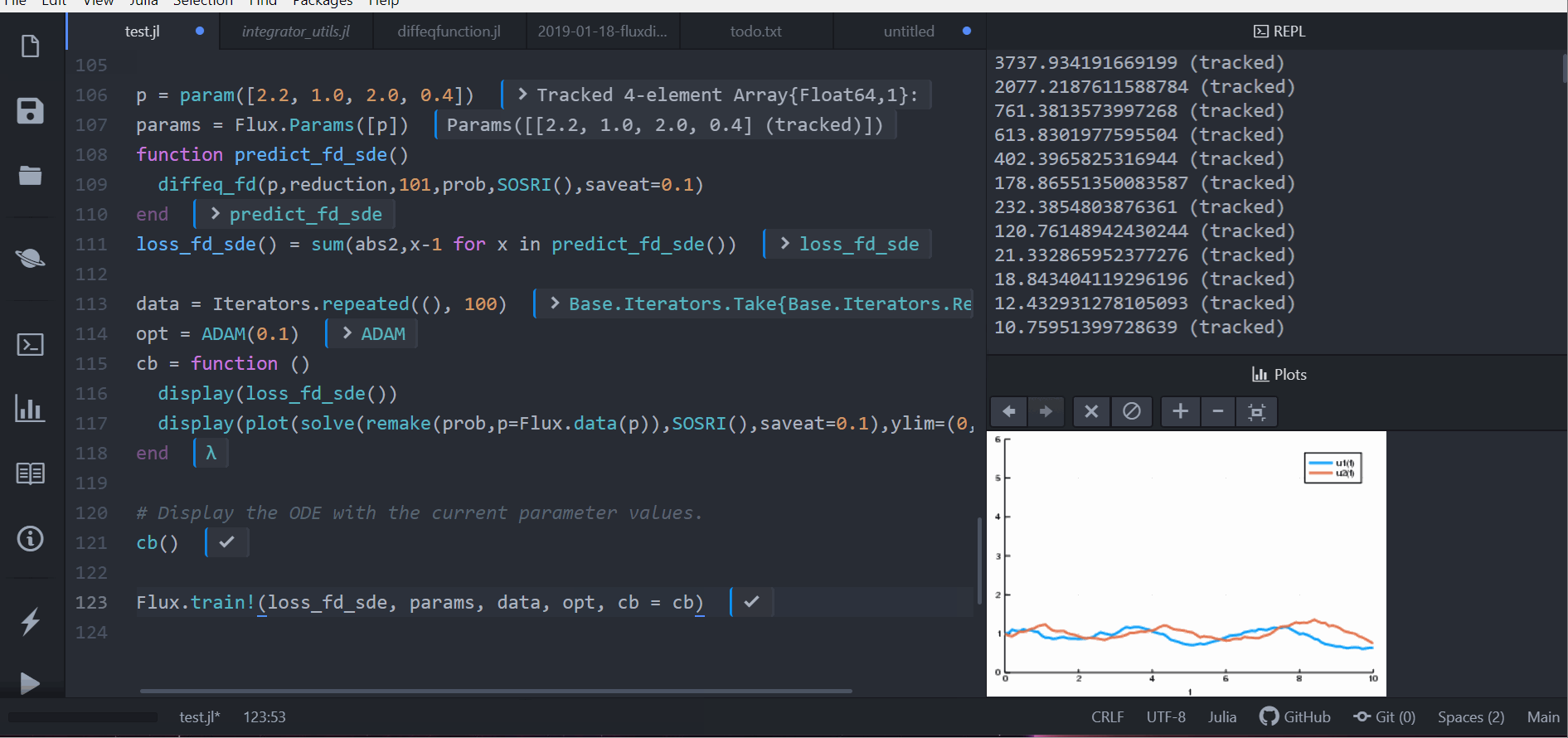

SDE NN Animation

此代码可在模型库中找到

我们可以继续。有 在生物模拟中使用分段常数 的微分方程，或者有 来自金融模型的跳跃扩散方程，并且求解器通过 DiffEqFlux.jl 直接映射到 Flux 神经网络框架。DiffEqFlux.jl 只使用大约 100 行代码来实现这一切。

在 Julia 中实现神经 ODE 层

让我们退一步，现在在 Julia 中实现神经 ODE 层。请记住，这只是一个 ODE，其中导数函数本身由神经网络定义。为此，让我们首先定义导数的神经网络。在 Flux 中，我们可以定义一个具有 1 个隐藏层和 tanh 激活函数的多层感知器，例如

dudt = Chain(Dense(2,50,tanh),Dense(50,2))

要定义 NeuralODE 层，我们只需要提供一个时间跨度，并使用 NeuralODE 函数

tspan = (0.0f0,25.0f0)
node = NeuralODE(dudt,tspan,Tsit5(),saveat=0.1)

作为旁注，要在 GPU 上运行它，只需要让初始条件和神经网络位于 GPU 上。这会导致整个 ODE 求解器的内部操作在 GPU 上进行，而无需在集成方案中进行额外的数据传输。这看起来像

node = NeuralODE(gpu(dudt),tspan,Tsit5(),saveat=0.1)

通过示例了解神经 ODE 层的行为

现在，让我们在一个例子中使用神经 ODE 层来了解它的含义。首先，让我们在等距时间点生成 ODE 的时间序列。我们将使用神经 ODE 论文中的测试方程。

u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.5f0)

function trueODEfunc(du,u,p,t)
    true_A = [-0.1 2.0; -2.0 -0.1]
    du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),saveat=t))

现在，让我们将一个神经 ODE 与这些数据进行对比。为此，我们将定义一个单层神经网络，该网络只包含与之前相同的神经 ODE（但降低容差以帮助它收敛得更近，这使得动画更好看！）。

dudt = Chain(x -> x.^3,
             Dense(2,50,tanh),
             Dense(50,2))
n_ode = NeuralODE(dudt,tspan,Tsit5(),saveat=t,reltol=1e-7,abstol=1e-9)
ps = Flux.params(n_ode)

请注意，NeuralODE 与生成数据的解具有相同的时间跨度和 saveat。这意味着，给定一个 x（和初始值），它将生成一个它认为时间序列将是什么的猜测，其中动力学（结构）由内部神经网络预测。让我们看看它在训练网络之前给出的时间序列。由于 ODE 有两个因变量，我们将通过只显示第一个来简化绘图。绘图代码如下

pred = n_ode(u0) # Get the prediction using the correct initial condition
scatter(t,ode_data[1,:],label="data")
scatter!(t,pred[1,:],label="prediction")

Neural ODE Start

但是现在让我们训练我们的神经网络。为此，像以前一样定义一个预测函数，然后定义预测值和数据之间的损失

function predict_n_ode()
  n_ode(u0)
end
loss_n_ode() = sum(abs2,ode_data .- predict_n_ode())

现在我们训练神经网络，并观察它如何学习预测我们的时间序列。

data = Iterators.repeated((), 1000)
opt = ADAM(0.1)
cb = function () #callback function to observe training
  display(loss_n_ode())
  # plot current prediction against data
  cur_pred = predict_n_ode()
  pl = scatter(t,ode_data[1,:],label="data")
  scatter!(pl,t,cur_pred[1,:],label="prediction")
  display(plot(pl))
end

# Display the ODE with the initial parameter values.
cb()

Flux.train!(loss_n_ode, ps, data, opt, cb = cb)

Neural ODE Train

此代码可在模型库中找到

请注意，我们没有学习微分方程的解。相反，我们学习的是生成微分方程解的微小微分方程系统。即，neural_ode 层内部的神经网络学习了这个函数。

u' = A*u^3

因此，**它学习了时间序列工作机制的紧凑表示**，并且可以轻松地推断出不同初始条件下的情况。不仅如此，它还是一种非常灵活的方法，可以学习这种表示。例如，如果您的数据在时间点 `t` 上是不均匀间隔的，只需传入 `saveat=t`，ODE 求解器就会处理它。

正如您可能已经猜到，DiffEqFlux.jl 拥有各种额外的相关好东西，例如神经 SDE ( `NeuralSDE` )，供您在应用程序中探索。

核心技术挑战：通过微分方程求解器进行反向传播

最后，让我们解释一下需要解决的技术问题，以便让这一切成为可能。任何神经网络框架的核心都是反向传播导数的能力，以便计算损失函数关于网络参数的梯度。因此，如果我们将 ODE 求解器作为神经网络中的一个层，我们需要反向传播它。

有多种方法可以做到这一点。最常见的方法称为（伴随）灵敏度分析。灵敏度分析定义了一个新的 ODE，它的解给出成本函数关于参数的梯度，并求解这个辅助 ODE。这是神经常微分方程论文中讨论的方法，但实际上可以追溯到更早，流行的 ODE 求解器框架，如 FATODE 、 CASADI 和 CVODES 已经使用这种伴随方法很长时间了（CVODES 诞生于 2005 年！）。DifferentialEquations.jl 也实现了灵敏度分析

伴随灵敏度分析方法的效率问题在于，它们需要多次对 ODE 进行正向求解。正如您所料，这非常昂贵。像 CVODES 中的检查点方案这样的方法通过保存更近的时间点来减少成本，从而使正向解更短，但代价是使用更多内存。神经常微分方程论文中的方法试图通过对 ODE 本身进行反向求解以及伴随求解来消除对这些正向解的需要。这个问题是，这种方法隐式地假设 ODE 集成器是 可逆的。遗憾的是，对于一阶 ODE，没有可逆的自适应集成器，因此没有 ODE 求解器方法可以保证这一点。例如，这里有一个快速方程，其中使用论文中的 Adams 方法对 ODE 进行反向求解在其最终点具有 >1700% 的误差，即使求解器容差为 1e-12

using Sundials, DiffEqBase
function lorenz(du,u,p,t)
 du[1] = 10.0*(u[2]-u[1])
 du[2] = u[1]*(28.0-u[3]) - u[2]
 du[3] = u[1]*u[2] - (8/3)*u[3]
end
u0 = [1.0;0.0;0.0]
tspan = (0.0,100.0)
prob = ODEProblem(lorenz,u0,tspan)
sol = solve(prob,CVODE_Adams(),reltol=1e-12,abstol=1e-12)
prob2 = ODEProblem(lorenz,sol[end],(100.0,0.0))
sol = solve(prob,CVODE_Adams(),reltol=1e-12,abstol=1e-12)
@show sol[end]-u0 #[-17.5445, -14.7706, 39.7985]

（这里我们再次使用来自 SUNDIALS 的 CVODE C++ 求解器，因为它们与神经 ODE 论文中使用的 SciPy 集成器非常匹配。）

这种不准确性是神经 ODE 论文中的方法没有在软件套件中实现的原因，但它再次突出了一个细节。并非所有 ODE 都会因这个问题而产生较大误差。对于没有问题的 ODE，这将是执行伴随灵敏度分析的最有效方法。而且这种方法只适用于 ODE。不仅如此，它甚至不适用于所有 ODE。例如，具有不连续性（事件）的 ODE 被推导的假设所排除。因此，我们再次得出结论，一种方法是不够的。

在 DifferentialEquations.jl 中，我们实现了多种方法来计算微分方程关于参数的导数。我们有一个最近的预印本详细介绍了其中的一些结果。我们发现的一件事是，直接使用自动微分可以成为最有效和最灵活的方法之一。Julia 的 ForwardDiff.jl、Flux 和 ReverseDiff.jl 可以直接应用于对原生 Julia 微分方程求解器本身执行自动微分，这可以提高性能，同时提供新的功能。我们的研究结果表明，当微分方程中的参数少于 100 个时，前向模式自动微分速度最快，而对于 >100 个参数，伴随灵敏度分析效率最高。即使如此，我们有充分的理由相信，下一代通过源到源 AD、Zygote.jl 的反向模式自动微分将比所有伴随灵敏度实现更有效用于大量参数。

总而言之，能够在不同梯度方法之间切换而无需更改其余代码对于拥有一个可扩展、优化和可维护的框架来集成微分方程和神经网络至关重要。而 DiffEqFlux.jl 正是为用户提供了对此的直接访问。有三个具有类似 API 的函数

  • diffeq_rd 使用 Flux 的反向模式 AD 通过微分方程求解器。

  • diffeq_fd 使用 ForwardDiff.jl 的前向模式 AD 通过微分方程求解器。

  • diffeq_adjoint 使用伴随灵敏度分析来“反向传播 ODE 求解器”。

因此，要从反向模式 AD 层切换到前向模式 AD 层，只需更改一个字符。由于基于 Julia 的自动微分作用于 Julia 代码，因此原生 Julia 微分方程求解器将继续从该领域的进展中受益。

结论

机器学习和微分方程注定会走到一起，因为它们以互补的方式描述了非线性世界。在 Julia 生态系统中，我们以一种方式合并了微分方程和深度学习包，使这两个领域中的新独立开发可以直接一起使用。我们才刚刚开始了解这种软件所带来的可能性。我们希望未来的博客文章将详细介绍一些混合了这两个学科的酷炫应用程序，例如将我们即将推出的药代动力学模拟引擎 PuMaS.jl 嵌入到深度学习框架中。通过访问 ODE、SDE、DAE、DDE、PDE、离散随机方程等的完整求解器范围，我们很想知道您将使用 Julia 构建什么样的下一代神经网络。

注意：本文的可引用版本已发布在 Arxiv 上。

@article{DBLP:journals/corr/abs-1902-02376,
  author    = {Christopher Rackauckas and
               Mike Innes and
               Yingbo Ma and
               Jesse Bettencourt and
               Lyndon White and
               Vaibhav Dixit},
  title     = {DiffEqFlux.jl - {A} Julia Library for Neural Differential Equations},
  journal   = {CoRR},
  volume    = {abs/1902.02376},
  year      = {2019},
  url       = {https://arxiv.org/abs/1902.02376},
  archivePrefix = {arXiv},
  eprint    = {1902.02376},
  timestamp = {Tue, 21 May 2019 18:03:36 +0200},
  biburl    = {https://dblp.org/rec/bib/journals/corr/abs-1902-02376},
  bibsource = {dblp computer science bibliography, https://dblp.org}
}