DiffEqFlux.jl – Julia 的神经微分方程工具包

2019年4月4日 | Chris Rackauckas, Mike Innes, Yingbo Ma, Jesse Bettencourt, Lyndon White, Vaibhav Dixit，译者：杜岳华（Yueh-Hua Tu）Dboy Liao (Yin-Chen Liao)

在这篇文章中，我们将展示在 Julia 中使用微分方程求解器（DiffEq solver）搭配神经网络是多么简单、有效而且稳定。

Flux ODE 訓練動畫

Neural Ordinary Differential Equations，在这篇文章获得 NeurIPS 2018 最佳论文奖的殊荣之前，其早已成为热门话题。 这篇论文给出了许多令人赞赏的结果，它结合了两个不相干的领域，但这仅仅是个开始而已： 神经网络与微分方程简直天生绝配。这篇文章来自 Flux 工具包的作者与 DifferentialEquations.jl 工具包作者的合作，实现 Neural ODEs 论文, 将解释为什么这个项目会诞生，以及这个项目现在和未来的走向，也会开始描绘极致的工具会有怎样的可能性。

Julia 中运用数值方法来解微分方程的 DifferentialEquations.jl 函数库的众多优势已经在其他文章中被详细讨论。 除了经典 Fortran 方法的众多性能评测之外， 它包含了其他新颖的功能，像是 GPU 加速、 分布式（多节点）并行运算 以及精密的事件处理。 最近，这些 Julia 土生土长的微分方程方法已经成功地整合进 Flux 深度学习工具包， 并允许在神经网络中使用整套完整测试、优化的 DiffEq 方法。 我们将使用新工具包 DiffEqFlux.jl 展示给读者， 在神经网络中增加微分方程层是多么简单，并可以使用一系列微分方程方法， 包含刚性（stiff）常微分方程、随机微分方程、延迟微分方程，以及混合（非连续）微分方程。

这是第一个完美结合完整微分方程方法及神经网络模型的工具包。这篇文章将说明为什么完整微分方程 方法套组的弹性如此重要。能够融合神经网络及 ODEs、SDEs、DAEs、DDEs、刚性方程， 以及像伴随灵敏度运算（adjoint sensitivity calculations）这样不同的方法， 这是一个神经微分方程重大的广义化工作，将来提供更好的工具让研究者去探索问题领域。

（注：如果你对这个工作有兴趣，同时是大学或是研究所学生， 我们有 提供 Google Summer of Code 项目。 并且 暑假过后有丰厚的津贴补贴。 请加入 Julia Slack 的 #jsoc 频道，欢迎更进一步的细节讨论。）

  1. 微分方程究竟与神经网络有何关联？
  2. 什么是神经微分方程（ODE）？
  3. 那要怎么解微分方程呢？
  4. 让我们把微分方程放到神经网络架构里吧！
  5. 完整的 ODE 求解工具对于这个应用为什么是必须的呢？
  6. 究竟有多少种不同的微分方程呢？
  7. 用 Julia 实现一个常微分方程神经网络层
  8. 用例子理解常微分神经网络的行为
  9. 核心的技术问题：微分方程求解器的反向传播
  10. 结论

微分方程究竟与神经网络有何关联？

对于不熟悉相关领域的人来说，想必第一个问题自然是：为什么微分方程在神经网络这个脉络下，会有举足轻重的关联？ 简而言之，微分方程可以借助数学模型来叙述、编码 (encoding) 先验的结构化假设，来表示任何一种非线性系统。

让我们稍稍解释一下最后这句话在说什么。一般来说，主要有三种方法来定义一个非线性转换: 直接数学建模、机器学习与微分方程式。 直接数学建模可以直接写下输入与输出间非线性转换，但只有在输入与输出间函数关系形式为已知时可用， 然而大部分的状况，两者间的确切关系并不是事先知道的。所以大多数的问题是， 你如何在输入输出间的关系未知的情况下，来对其做非线性数学建模？

其中一种解决方法是使用机器学习算法。典型的机器学习处理的问题里，会给定一些输入数据 x 和你想预测的输出 y。 而由给定 xx 产生预测值 yy 就是一个机器学习模型（以下称作 MLML）。 在训练阶段，我们想办法调整 MLML 的参数让它得以产生更正确的预测值。 接下来，我们即可用 MLML 进行推理 (即针对事前没见过的 xx 值去产生相对对应的 yy)。 同时，这也不过是一个非线性转换而已 y=ML(x)y=ML(x)。 但是 MLML 有趣的地方在于它本身数学模型的形式可以非常基本但却可以调整适应至各种数据。 举例来说，一个简单的以 sigmoid 函数作为激活函数的神经网络模型（以设计矩阵的形式，design matrix）， 本质上来说就是简单的矩阵运算复合带入 sigmoid 函数里。 举例来说，ML(x)=σ(W3⋅σ(W2⋅σ(W1⋅x)))ML(x)=σ(W3⋅σ(W2⋅σ(W1⋅x))) 即是一个简单的三层神经网络模型， 其中 W=(W1,W2,W3)W=(W1, W2, W3) 为可以被调整的模型参数。 接下来即是选择适当的 W 使得 ML(x)=yML(x)=y 可以合理的逼近收集到的数据。 相关机器学习理论已经保证了这是一个估计非线性系统的一个好方法。 举例来说，Universal Approximation Theorem 说明了只要有足够的层数或参数（即够大的 W 矩阵）， ML(x) 可以逼近任何非线性函数 (在常见的限制条件下)。

这太好了，它总是有解！然而有几个必须注意的地方，主要在于这模型需直接从数据里学习非线性转换。 但在大多数的状况，我们并不知晓实际的非线性方程整体，但我们却可以知道它的结构细节。 举例来说，这个非线性转换可以是关于森林里的兔子的数量，而我们可能知道兔子群体出生率正比于其数量。 因此，与其从无到有去学习兔子群体数量的非线性模型，我们或许希望能够套用这个数量与出生率的已知*先验（a priori）关系， 和一组参数来描绘它。对于我们的兔子群体模型来说，可以写成

rabbits(明日)=Model(rabbits(今日)).\text{rabbits(明日)} = \text{Model}(\text{rabbits(今日)}).

在这个例子裡，我们得知群体出生率正比于群体数量这个先验知识。 而如果用数学的方式去描述这个关于兔子群体大小结构的假设，即是微分方程。 在这里，我们想描绘的是准确地说，是在给定的某一時間点的兔子群体出生率将会随着兔子群体大小的增加而增加。 简单地写的话，可以写成以下的式子

rabbits′(t)=α⋅rabbits(t)\text{rabbits}'(t) = \alpha\cdot \text{rabbits}(t)

其中， α\alpha 是可以学习调整的参数。如果你还记得以前学过的微积分， 这个方程的解即为增长率为 α\alpha 的指数增长函数

rabbits(tstart)e(αt)\text{rabbits}(t_\text{start})e^{(\alpha t)}

其中 rabbits(tstart)\text{rabbits}(t_\text{start}) 为初始的兔子数量。但值得注意的是，其实我们并不需要知道这个微分方程的解 才能验证以下想法：我们只需描绘模型的结构条件，数学即可帮助我们求解出这个解应该有的样子。 基于这个理由，使得微分方程成为许多科学领域的工具。例如物理学的基本定律明述了电荷的作用力 (麦克斯韦方程组)。 这些方程组对于物体的变化方式是重要的方程组，因此这些方程组的解即是物体将会在哪里的预测结果。

但在近十年这些应用已经有了长足的发展，随着像是系统生物学（systems biology）领域的兴起， 整合已知的生物结构以及数学上列举的假设，以学习到关于细胞间相互作用的知识， 或是系统药理学（systems pharmacology）中通过对一些特定药物剂量 PK/PD 的建模。

所以随着我们的机器学习模型不断发展，会渴求更多更大量的 数据， 微分方程因此成为一个很有吸引力的选项，用来指定一个可学习（通过参数）但又有限制条件的非线性变换。 它们将是整合既有结构关系的领域知识，以及输入输出之间非常重要的一种方式。 有这样的一种方法和观点看待两者，两种方法都有其需要权衡的优缺点， 可以让彼此成为建模上互补的方法。 这看起来是一条开始将科学实践与机器学习两相结合的明显道路，期待未来会有崭新而令人兴奋的未来！

什么是神经微分方程（ODE）？

神经微分方程只是众多结合这两个领域的方法之一。 最简单的解释方法就是，并不是直接去学习非线性变换，我们希望去学习非线性变换的结构。 如此一来，不用去计算 y=ML(x)y=ML(x)，我们将机器学习模型放在导数项上 y′(x)=ML(x)y'(x) = ML(x)，然后我们求解微分方程。 为什么这么做？一个动机就是，这样定义的模型，然后用最简单、最容易出错的方式，欧拉法（Euler method）， 求解微分方程，你将会得到与残差神经网络（residual neural network）等价的结果。 欧拉法的工作原理是基于 y′(x)=dydxy'(x) = \frac{dy}{dx} 这个事实，因此，

Δy=(ynext−yprev)=Δx⋅ML(x)\Delta y = (y_\text{next} - y_\text{prev}) = \Delta x\cdot ML(x)

则会导出

yi+1=yi+Δx⋅ML(xi)y_{i+1} = y_{i} + \Delta x\cdot ML(x_{i})

这在结构上类似于 ResNet，最成功的图像处理模型之一。 Neural ODEs 论文的洞察力在于，更深、更强大的类似 ResNet 的模型可以有效地逼近类似于“无限深”，如同每一层趋近于零的模型。 我们可以直接构建微分方程，而不是通过增加层数这种手段，随后用专门的微分方程方法求解。 数值微分方程方法是一门可以追溯到第一台计算机出现时期的科学，而现代方法可以动态调整步长 Δx\Delta x， 以及使用高阶逼近的方法来大幅减少实际需要的步数。并且事实证明，它在实践中也运行得很好。

那要怎么解微分方程呢？

首先，如何求解微分方程的数值解呢？如果你是在求解微分方程方面的新手， 你可能想要参考我们的用 Julia 求解微分方程视频教程， 以及参考我们的DifferentialEquations.jl 微分方程教程手册。 概念是这样的，如果你通过导函数 u'=f(u,p,t) 定义一个 ODEProblem， 接着就能用初始条件 u0 、时间段 tspan，以及相关的参数 p 去求解这个问题。

举个例子，Lotka-Volterra 方程描述了野兔和狼种群的动态关系。 它们可以被写成：

x′=αx+βxyx^\prime = \alpha x + \beta x y y′=−γy+γxyy^\prime = -\gamma y + \gamma x y

进一步转换成 Julia 会像：

using DifferentialEquations
function lotka_volterra(du,u,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = α*x - β*x*y
  du[2] = dy = -δ*y + γ*x*y
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)

然后要解微分方程，你可以简单地调用 solve 来处理 prob：

sol = solve(prob)
using Plots
plot(sol)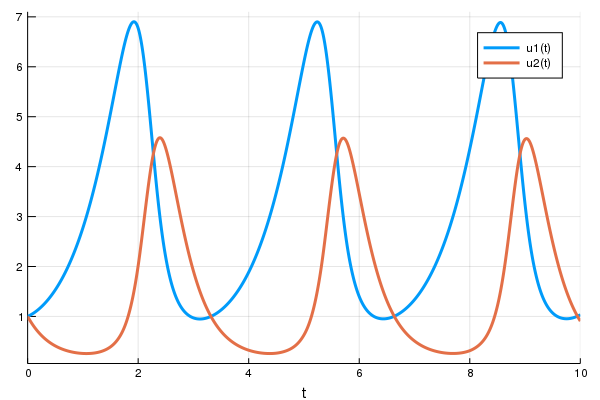

LV Solution Plot

最后一件要说的事情就是我们可以让我们的初始条件（u0）以及时间区间（tspans） 成为参数（p 的元素）的函数。举例来说，我们可以这样定义 ODEProblem：

u0_f(p,t0) = [p[2],p[4
tspan_f(p) = (0.0,10*p[4])
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0_f,tspan_f,p)

如此一来，关于这个问题的所有东西都由参数向量决定（p，或是文献中的 θ）。 这东西的用途会在后续彰显出来。

DifferentialEquations.jl 提供非常多强大的选项以供自定义， 像是精度（accuracy）、容忍度（tolerances）、微分方程方法、事件等等；可以参考 手册以获得更多进阶的使用方式。

让我们把微分方程放到神经网络架构里吧！

要理解一个微分方程是怎么样被嵌入到一个神经网络中，那我们就要看看一个神经网络层实际上是什么。 一个层实际上就是一个可微分函数，它会吃进一个大小为 n 的向量，然后吐出一个大小为 m 的新向量。 就这样！网络层传统上是使用简单的函数，像是矩阵相乘，但有了可微分编程的精神， 人们越来越倾向实验复杂的函数，像是光线追踪以及物理引擎。

恰巧微分方程方法也符合这样的架构：一个方法会吃进某个向量 p （它有可能包含一些参数像是初始起点），然后输出某个新向量，也就是解。 而且它还是可微分的，这代表我们可以直接把他推进大型可微分程序内。 这个大型程序可以开心地容纳神经网络，以及我们可以继续使用标准优化技巧， 像是 ADAM 来优化那些权重。

DiffEqFlux.jl 让这件事做起来很简单；我们一起动手做！ 我们就一如往常地开始解这个方程式，不需要计算梯度。

p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)
sol = solve(prob,Tsit5(),saveat=0.1)
A = sol[1,:] # length 101 vector

我们一起将微分方程的解画在 (t,A) 坐标轴上，一起看看我们得到什么：

plot(sol)
t = 0:0.1:10.0
scatter!(t,A)

Data points plot

在 solve 中的一个好的设计是，它会处理类型的兼容性，让它可以兼容于神经网络框架（Flux）。 要证明这个，我们来用函数定义一层神经网络，然后还有一个损失函数，是输出值相对 1 距离的平方。 在 Flux 中，他看起来像这样：

p = [2.2, 1.0, 2.0, 0.4] # 初始參數向量
params = Flux.params(p)

function predict_rd() # 我們的單層神經網路
  solve(prob,Tsit5(),p=p,saveat=0.1)[1,:]
end

loss_rd() = sum(abs2,x-1 for x in predict_rd()) # 損失函數

现在我们会叫 Flux 来训练神经网络，借由跑 100 epoch 来最小化我们的损失函数（loss_rd()）， 因此，可以得到优化的参数：

data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function () # 用 callback function 來觀察訓練情況
  display(loss_rd())
  # 利用 `remake` 來再造我們的 `prob` 並放入目前的參數 `p`
  display(plot(solve(remake(prob,p=p),Tsit5(),saveat=0.1),ylim=(0,6)))
end

# 顯示初始參數的微分方程
cb()

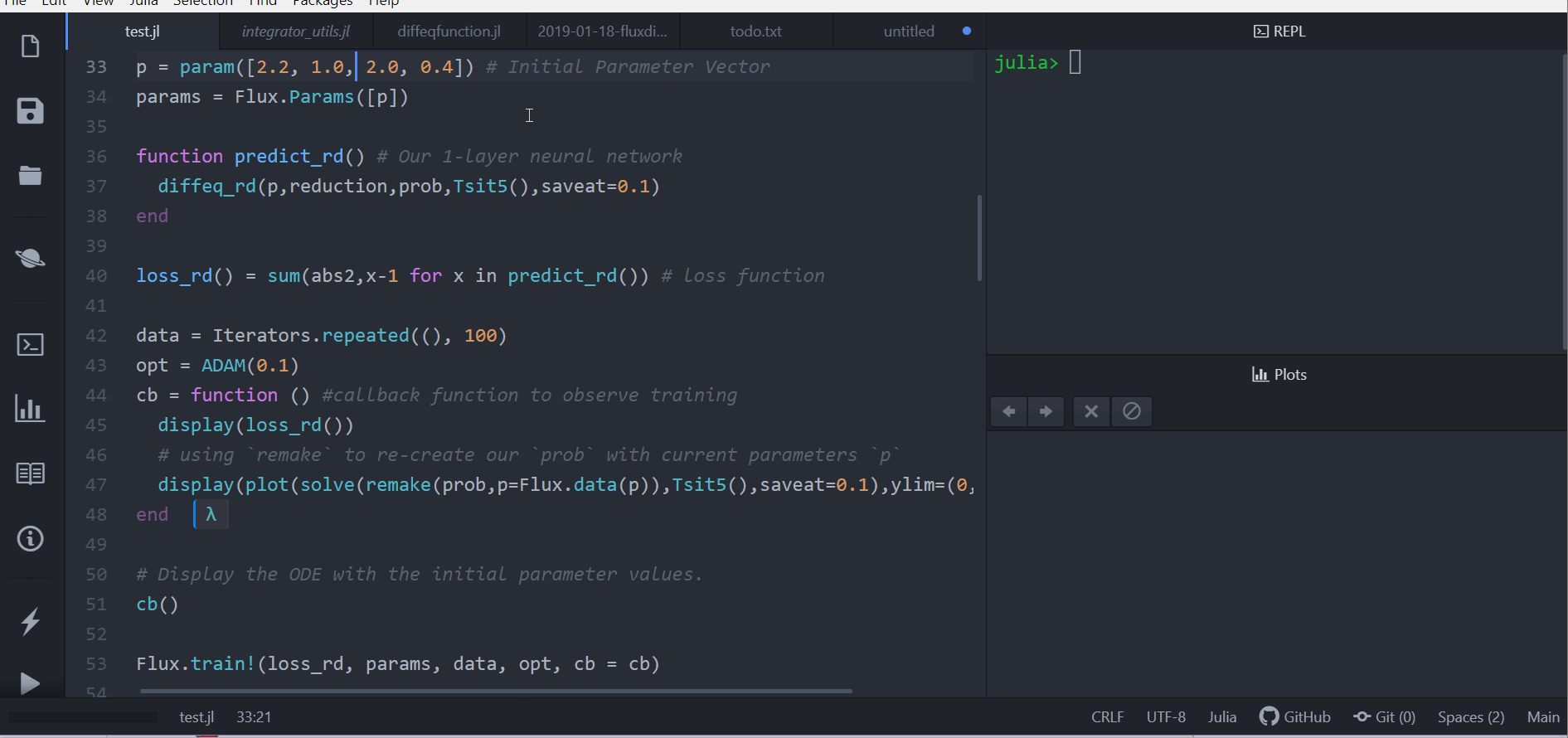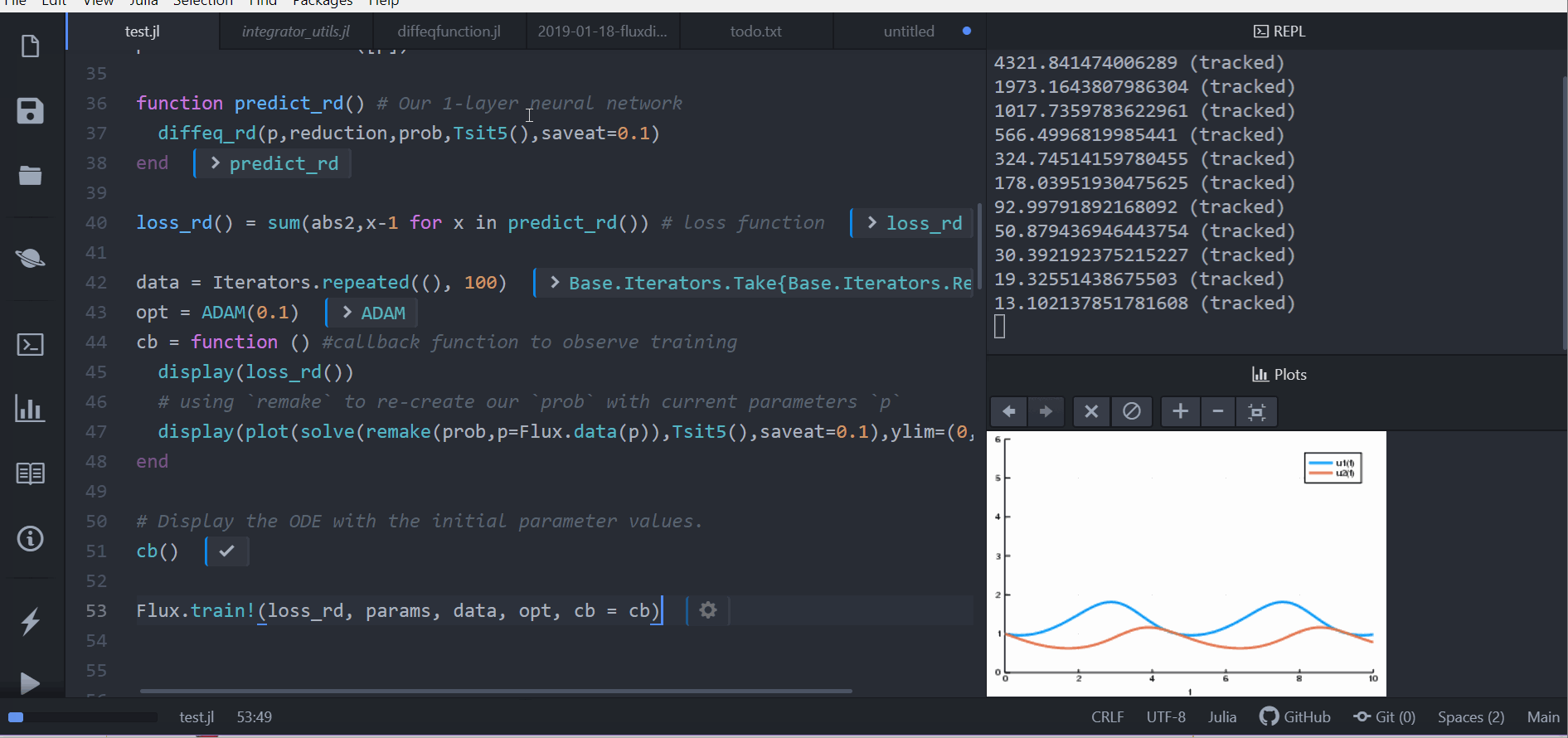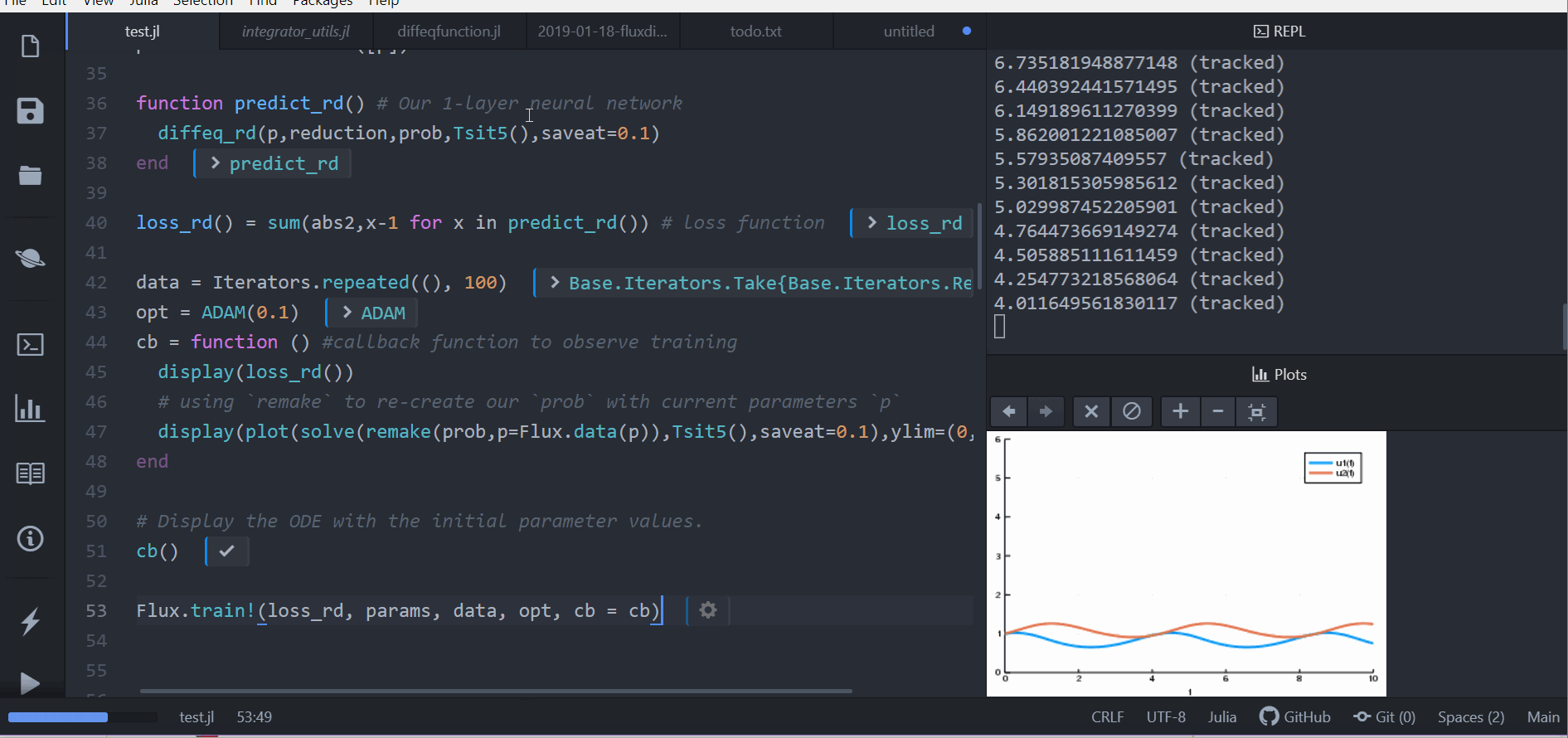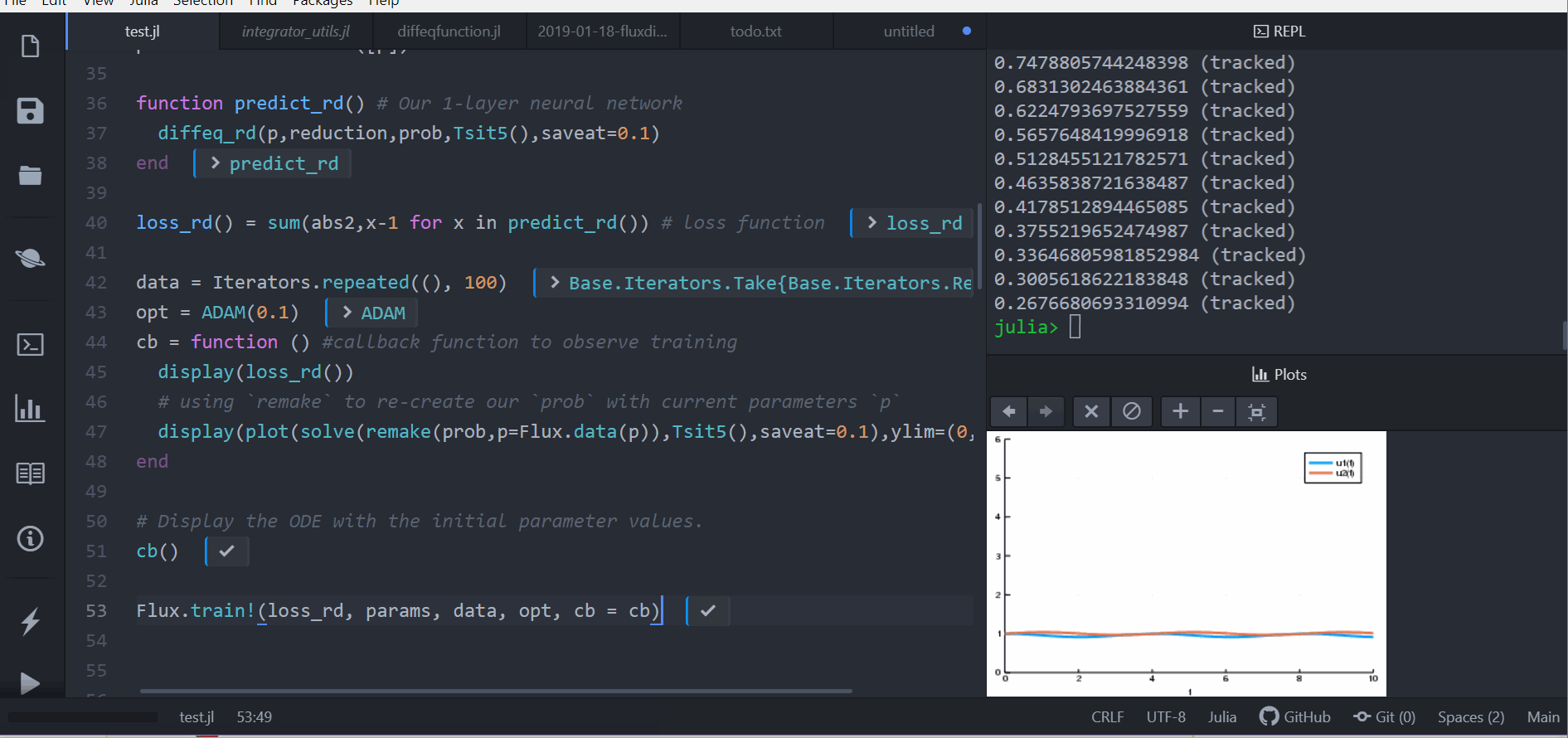
Flux.train!(loss_rd, params, data, opt, cb = cb)

结果会以动画显示在上面。 这些代码会被放在 model-zoo

Flux 在寻找可以最小化损失函数的神经网络参数（p），也就是，他会训练神经网络： 整个过程是这样的，在神经网络中向前传递（forward pass）的过程也包含了解微分方程的过程。 我们的损失函数会惩罚当兔子数量远离 1 的时候， 所以我们的神经网络会找到兔子以及狼的族群都是常数 1 的时候的参数。

现在，我们已经把微分方程作为一层网络解完了，我们可以随意将他添加到任何地方。 举例来说，多层感知器（multilayer perceptron）可以用 Flux 写成像这样

m = Chain(
  Dense(28^2, 32$, relu),
  Dense(32, 10),
  softmax)

而且，假如我们有个带有合适大小的参数向量的 ODE ，我们可以像这样把他代入我们的模型中：

m = Chain(
  Dense(28^2, 32, relu),
  # this would require an ODE of 32 parameters
  p -> solve(prob,Tsit5(),p=p,saveat=0.1)[1,:],
  Dense(32, 10),
  softmax)

抑或是，我们也可以把他代入到卷积神经网络中，使用前一层卷积层的输出当作 ODE 的初始条件使用：

m = Chain(
  Conv((2,2), 1=>16, relu),
  x -> maxpool(x, (2,2)),
  Conv((2,2), 16=>8, relu),
  x -> maxpool(x, (2,2)),
  x -> reshape(x, :, size(x, 4)),
  x -> solve(prob,Tsit5(),x=x,saveat=0.1)[1,:],
  Dense(288, 10), softmax) |> gpu

只要你可以写下 forward pass，我们就可以处理任何参数化的可微分程序并优化它。一个新世界即为你囊中之物啊。

完整的 ODE 求解工具对于这个应用为什么是必须的呢？

前文中，我们把现有的求解工具和深度学习结合在一起。反观另一个杰出的实现 torchdiffeq 采取了另一种实现方式，直接使用 pytorch 实现了许多求解算法，包含一个自适应的 Runge Kutta 4-5 (dopri5) 和一个 Adams-Bashforth-Moulton 方法 (adams)。然而，其中的实现对于特定的模型来说，虽可算是非常有效率地，但无法完整整合所有可行的求解工具，这带来了一些限制。

我们考虑以下这个例子：ROBER ODE。最被广泛测试过 (且优化) 过 Adams-Bashforth-Moulton 方法的实现是著名的 C++ 套件 SUNDIALS 中的 CVODE 积分器 (传统的 LSODE 的一个分支)。让我们用 DifferentialEquations.jl 去使用 CVODE 中的 Adams 方法来解这个 ODE 吧：

rober = @ode_def Rober begin
  dy₁ = -k₁*y₁+k₃*y₂*y₃
  dy₂ =  k₁*y₁-k₂*y₂^2-k₃*y₂*y₃
  dy₃ =  k₂*y₂^2
end k₁ k₂ k₃
prob = ODEProblem(rober,[1.0;0.0;0.0],(0.0,1e11),(0.04,3e7,1e4))
solve(prob,CVODE_Adams())

（熟悉使用 MATLAB 解 ODE 的读者来说，这与 ode113 类似）

包含 Ernst Hairer 的 Fortran 函数库中的 dopri 在内，这两种方法在求解这个问题上，都呈现停滞并无法得出结果。其症结在于，这个 ODE 为“刚性”，而当求解算法有着「较小的稳定区间」时，将无法对这类 ODE 求解（如读者想就细节进一步了解的话，我推荐 Hairer 所著的 Solving Ordinary Differential Equations II 一书）。

但另一方面，KenCarp4() 在求解这个问题上，只是一瞬间的事：

sol = solve(prob,KenCarp4())
using Plots
plot(sol,xscale=:log10,tspan=(0.1,1e11))

ROBER Plot

这不过是个积分法一些微小细节的范例：藉由 PI-自适应控制器和步距预测隐式解算器等，都有着复杂微小的细节并需要长时间的开发与测试，才能变成有效率并稳定的求解器。而不同的问题也会需要不同的方法：如为了在许多物理问题上得到够好的解并避免偏移，辛积分器是必须的；另外像是 IMEX 积分器 在求解偏微分方程上也是不可或缺的。由此可见建立一个具产品水准的求解器是有迫切需要，但目前相对稀少的。

在科学运算这个领域，常常会为了机器学习类型的的方法设计独立的函数库，但在 Julia 中里两者并无不同，也就是说明你可以直接利用这些现成的函数库。

究竟有多少种不同的微分方程呢？

常微分方程不过只是其中一种微分方程而已。有许多不同额外的特征是可以被加入到微分方程的结构式里。举例来说，兔子未来数量不是与现在的兔子数量有关，因为亲代兔子需要花一段时间怀孕，之后子代兔子才会出生。因此，实际上兔子的出生率应与过去的兔子数量有关。在原来的范例的微分方程中的导数加入一个延迟项，使得这组方程形成所谓的时滞微分方程 (DDE)。由于 DifferentialEquations.jl 使用与常微分方程相同的接口处理时滞微分方程，它也可以被当成 Flux 中的一层神经网络。这里是个范例：

function delay_lotka_volterra(du,u,h,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = (α - β*y)*h(p,t-0.1)[1]
  du[2] = dy = (δ*x - γ)*y
end
h(p,t) = ones(eltype(p),2)
u0 = [1.0,1.0]
prob = DDEProblem(delay_lotka_volterra,u0,h,(0.0,10.0),constant_lags=[0.1])

p = [2.2, 1.0, 2.0, 0.4]
params = Flux.params(p)

using DiffEqSensitivity
function predict_rd_dde()
  solve(prob,MethodOfSteps(Tsit5()),p=p,saveat=0.1,sensealg=TrackerAdjoint())[1,:]
end
loss_rd_dde() = sum(abs2,x-1 for x in predict_rd_dde())
loss_rd_dde()

这个范例的完整代码，包含产生动画在内，可以在 model-zoo 裡找到。

除此之外，我们也可以在微分方程中导入随机性去模拟随机事件如何影响预期的出生或死亡。 这类的微分方程被称为随机微分方程 (SDE)。 由於 DifferentialEquations.jl 同样也可以处理随机微分方程 (也是目前唯一一个包含刚性和非刚性随机微分方程解算器的函数库)， 也同样可以用类似方法引入 Flux 作为神经网络的一层。 以下是使用 SDE 作为神经网络一层的一个范例：

function lotka_volterra_noise(du,u,p,t)
  du[1] = 0.1u[1]
  du[2] = 0.1u[2]
end
prob = SDEProblem(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,10.0))

p = param([2.2, 1.0, 2.0, 0.4])
params = Flux.params(p)
function predict_sde()
  solve(prob,SOSRI(),p=p,sensealg=TrackerAdjoint(),saveat=0.1,
                     abstol=1e-1,reltol=1e-1)[1,:]
end
loss_fd_sde() = sum(abs2,x-1 for x in predict_sde())
loss_fd_sde()

接着我们可以训练这个神经网络去找出一组参数使得兔子数量成一个定值并观察中间变化的过程：

data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function ()
  display(loss_fd_sde())
  display(plot(solve(remake(prob,p=p),SOSRI(),saveat=0.1),ylim=(0,6)))
end

# 畫出當下參數的 ODE
cb()

Flux.train!(loss_fd_sde, params, data, opt, cb = cb)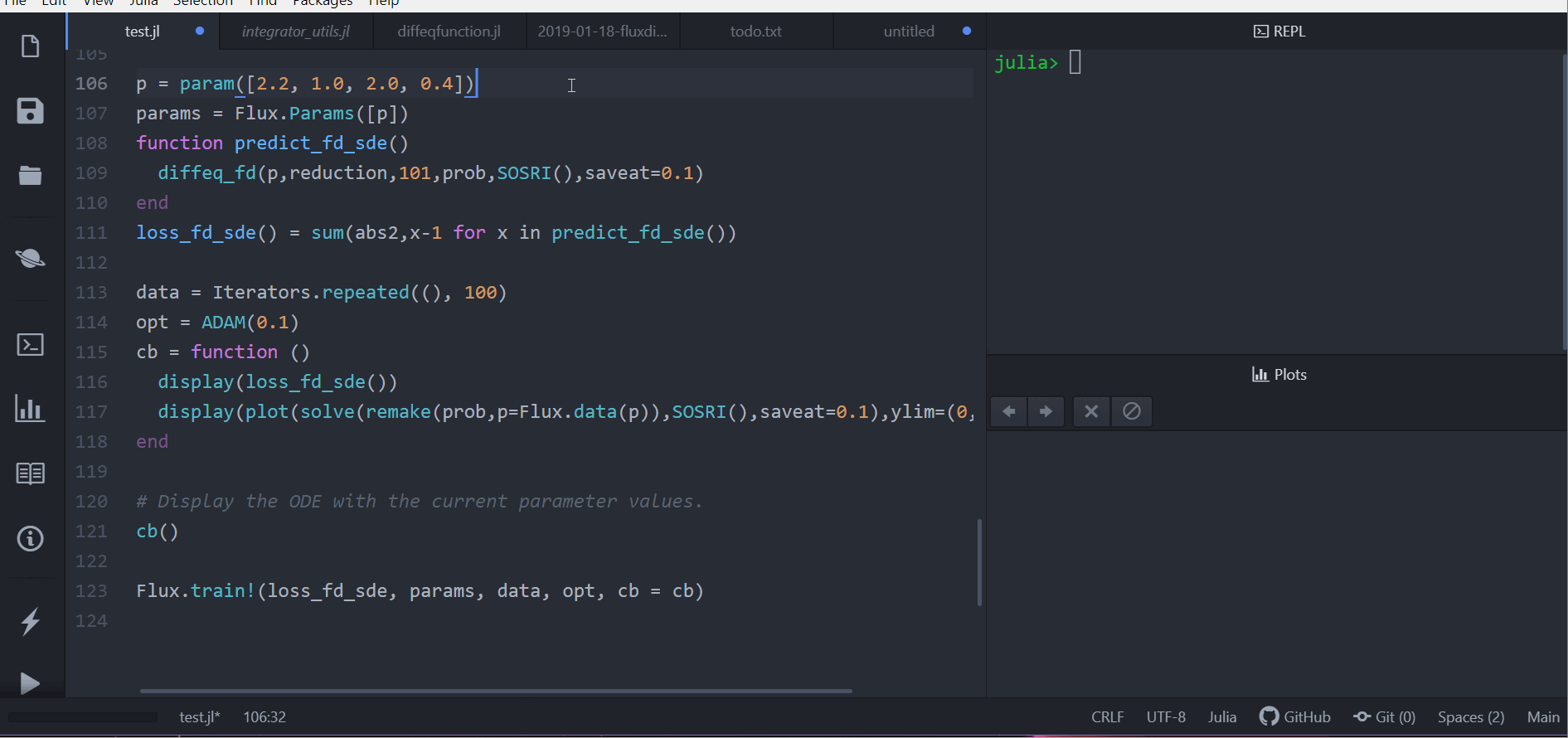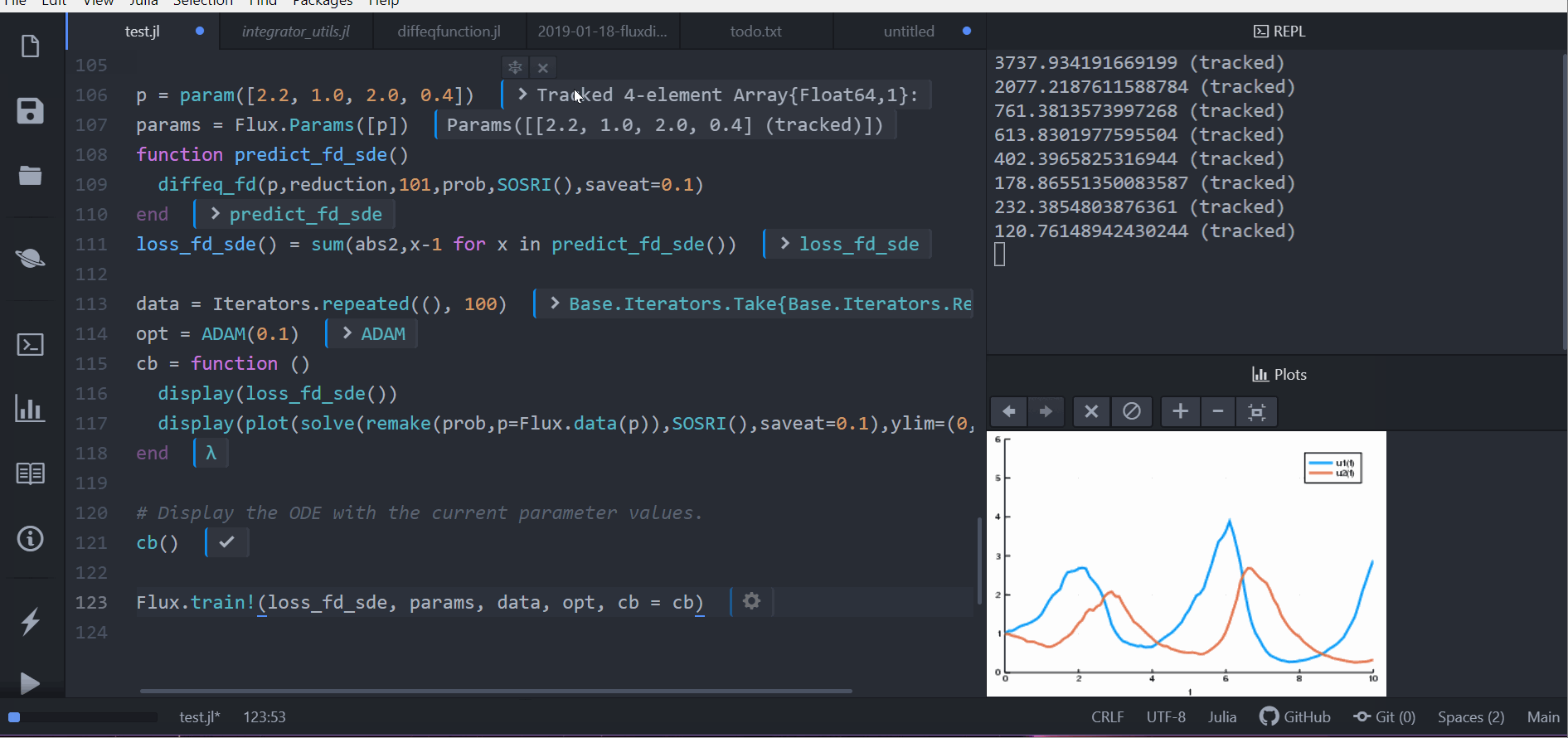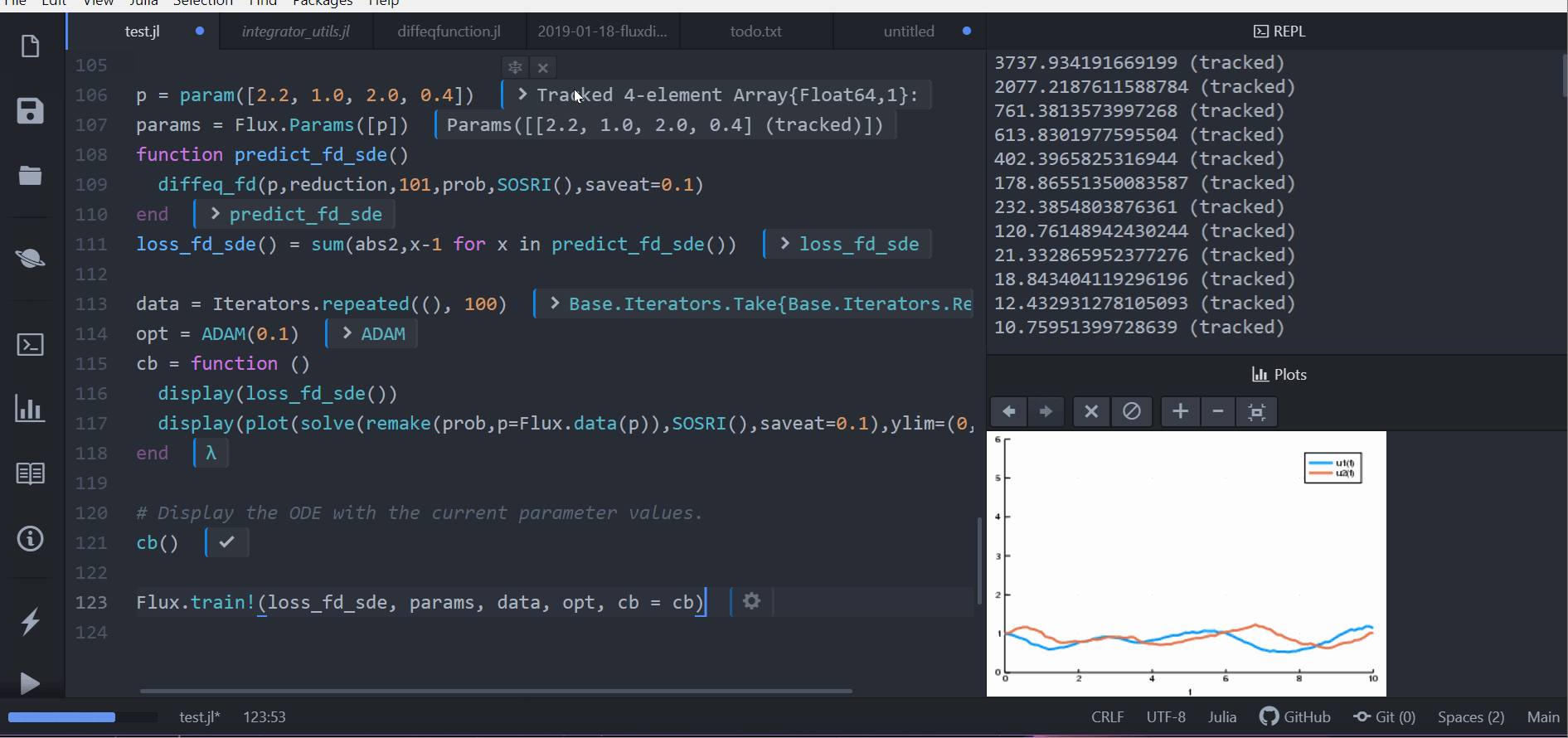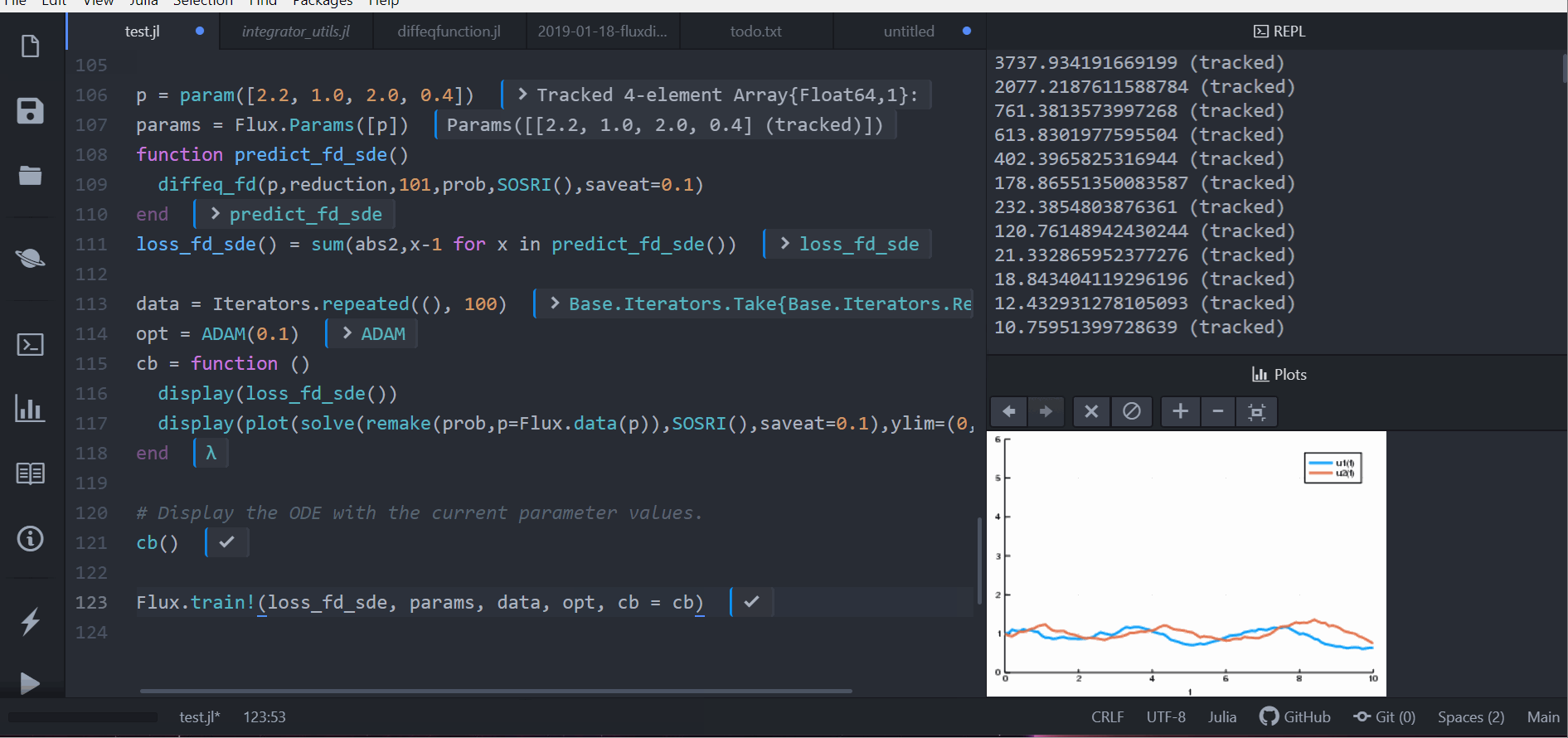

SDE NN Animation

This code can be found in the model-zoo

我们可以继续下去。譬如也些微分方程式是呈分片段常数函数 (piecewise constant)被使用在生物模拟上，抑或是被应用于财务模型中的跳跃扩散方程式 (jump diffusion)。而上述这些方程式解算器，都可以透过 FluxDiffEq.jl 很好地整合进 Flux 神经网络的架构裡，且 FluxDiffEq.jl 大约只使用了约 100 行左右的代码便完成了这些实现。

用 Julia 实现一个常微分方程神经网络层

现在我们回头用 Julia 实现一个常微分方程神经网络层吧！牢记这不过就是一个把常微分方程中的导数函数替换成一个神经网络层。为此，我们先来定义一个神经网络做为导数。在 Flux 中，我们可以以下的代码实现一个多层感知器，带有一层隐藏层和 tanh 作为 activation function：

dudt = Chain(Dense(2,50,tanh),Dense(50,2))

为了定义一个 NeuralODE，我们接着定义一个时间跨度并使用 NeuralODE 函数如下：

tspan = (0.0f0,25.0f0)
NeuralODE(dudt,tspan,Tsit5(),saveat=0.1)

顺便一提，如果想要在 GPU 上运算这个神经网络，只需让起始条件与神经网络架设于 GPU 上即可。在整合 GPU 的阶段，这会使得微分方程解算器内部运算直接在 GPU 上执行，无需额外的资料传输。这写起来会像是[1]：

NeuralODE(gpu(dudt),tspan,Tsit5(),saveat=0.1)

用例子理解常微分神经网络的行为

现在，让我们用一个例子来看看常微分神经网络层到底是什么样子。首先，让我们用一个常微分方程来产生一个均匀时间点的时间序列。在这里我们会使用论文中的例子。

u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.5f0)

function trueODEfunc(du,u,p,t)
    true_A = [-0.1 2.0; -2.0 -0.1]
    du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),saveat=t))

现在，我们可以用一个常微分神经网络去配适这个数据。为此，我们会定义一个如同上文提及的单层神经网络（但在這裡我們降低了誤差容忍值來讓模型近似得更接近数据，得以产生较好的动画）：

dudt = Chain(x -> x.^3,
             Dense(2,50,tanh),
             Dense(50,2))
n_ode = NeuralODE(dudt,tspan,Tsit5(),saveat=t,reltol=1e-7,abstol=1e-9)
ps = Flux.params(n_ode)

注意到，neural_ode 中使用和产生数据的常微分方程解相同的时间跨度与 saveat，所以它会在每个时间点针对神经网络预测的动态系统状态来产生一个预测值。让我们来看看最初这个神经网络会给出怎样的时间序列。由於这个常微分方程有两个应变数，为了简化画图的作业，我们只画出第一个应变数。代码如下：

pred = n_ode(u0) # 使用真實的初始值來產生預測值
scatter(t,ode_data[1,:],label="data")
scatter!(t,pred[1,:],label="prediction")

Neural ODE Start

现在让我们来训练我们的神经网络吧！为此，这里如同前文一般定义了一个预测函数、一个 loss 函数来评估我们的预测值与数据：

function predict_n_ode()
  n_ode(u0)
end
loss_n_ode() = sum(abs2,ode_data .- predict_n_ode())

接着，我们训练神经网络，并观察它如何学习预测我们的时间序列的过程：

data = Iterators.repeated((), 1000)
opt = ADAM(0.1)
cb = function () # 觀察資料用的 callback 函數
  display(loss_n_ode())
  # 畫出當下預測和資料
  cur_pred = predict_n_ode()
  pl = scatter(t,ode_data[1,:],label="data")
  scatter!(pl,t,cur_pred[1,:],label="prediction")
  display(plot(pl))
end

# 呈現初始參數下的常微分方程
cb()

Flux.train!(loss_n_ode, ps, data, opt, cb = cb)

Neural ODE Train

可以在 model-zoo 找到完整代码

注意到，我们并不是针对 ODE 的解去学习。反而，我们是在学习一个可以产生这组解的 ODE 系统。也就是，这个在 neural_ode 中的神经网络学到的是这个函数

它学到的是这组时间序列如何运作的一个完整的表示法，并且它可以轻易的使用不同的初始条件对接下来的值进行外插。除此之外，这是个可以学习这样的表示法非常弹性的架构。举例来说，如果你的数据有的不是均匀间隔的时间点 t，只需在你的 ODE 解算器中让 saveat=t，让解算器去处理这个问题即可。

你可能现在已经猜到了，DiffEqFlux.jl 中还有个其他所有各式各样额外相关的好东西像是神经随机微分方程 (neural_msde)，让你去在你的应用中去探索发现。

核心的技术问题：微分方程求解器的反向传播

最后，我们来解释一下为了让上述理论可行，必须解决的技术问题。 为了要能够计算损失函数对于网络参数的梯度，任何神经网络架构的核心就是可以去反向传递导数。 因此如果我们将一个微分方程求解器作为一层网络，那么我们需要反向传递通过它。

有很多方法可以实现它。最常见的叫做（伴随）敏感性分析（adjoint sensitivity analysis）。 敏感性分析定义了一个新的微分方程，它的解会给出损失函数对于参数的梯度， 并并且解这个衍生的微分方程。这个方法在 Neural Ordinary Differential Equations 论文中有被讨论到， 但事实上，我们将会时间倒回到更早之前，当时流行的微分方程求解器框架，像是 FATODE、 CASADI 以及 CVODES 已经使用伴随法一段时间了（CVODES 甚至从 2005 年就问世了！）。 DifferentialEquations.jl 也提供了敏感性分析的实现。

在伴随敏感性分析的效率性问题上，他们需要微分方程的多个解。 可预见的，这会非常花时间。像 CVODES 的方法，利用了检查点机制，藉由储存接近的时间点来推论解， 伴随著内存用量的增加，得以加速。在 Neural ODE 一文中所使用的方法，则尝试要以反向的伴随法来替代对前向方法的依赖。 然而衍生的问题则是，这个方法隐含地假设了微分方程积分器必须是可逆的。 令人失望的是，目前对于一阶微分方程尚不存在可逆的自适应积分器，所以没有这样的微分方程求解器可以用。 举例而言，作为快速的验证，在论文中针对这样的微分方程上使用反向解算器 Adams， 即便设定了 1e-12 的容忍度，还在最后一个点上就会产生 >1700% 的误差：

using Sundials, DiffEqBase
function lorenz(du,u,p,t)
 du[1] = 10.0*(u[2]-u[1])
 du[2] = u[1]*(28.0-u[3]) - u[2]
 du[3] = u[1]*u[2] - (8/3)*u[3]
end
u0 = [1.0;0.0;0.0]
tspan = (0.0,100.0)
prob = ODEProblem(lorenz,u0,tspan)
sol = solve(prob,CVODE_Adams(),reltol=1e-12,abstol=1e-12)
prob2 = ODEProblem(lorenz,sol[end],(100.0,0.0))
sol = solve(prob,CVODE_Adams(),reltol=1e-12,abstol=1e-12)
@show sol[end]-u0 #[-17.5445, -14.7706, 39.7985]

（这边我们再一次地使用了 SUNDIALS 的 CVODE C++ 求解器， 由於他们最接近於论文中所用的 SciPy 的积分器。）

如此不精确的结果说明了为什么神经微分方程论文中的方法并不是使用软件套件中的实现， 这再一次地凸显了这些小细节。而并非所有微分方程都在这个问题上有如此巨大的误差。 对于那些并不会造成问题的微分方程来说，伴随敏感性分析方法会是最有效率的。 除此之外，这个方法只能用於常微分方程上。不只是这样，它甚至不能被用於所有常微分方程。 举例来说，具有非连续性（事件）的常微分方程并不符合可微分这个假设。 目前为止，我们再一次得到了相同的总结，单一方法是不够的。

DifferentialEquations.jl 套件已经实现了非常多不同的方法来计算微分方程的参数微分。 在我们最近的 preprint 文章中，更详细地描述了这些结果。 我们发现到一件事，直接使用自动微分会是一个最有效而有弹性的方式。 Julia 的 ForwardDiff.jl、Flux，以及 ReverseDiff.jl 套件可以直接将自动微分 用在原生的 Julia 微分方程求解器上，而即使增加新功能也可以提升效率。 我们也证实前向模式自动微分在微分方程少於 100 个参数是最快的， 而对于多於 100 个参数伴随敏感性分析是最有效率的。 即便如此，我们有好的理由相信次世代反向模式 source-to-source 自动微分，Zygote.jl， 将会是在大量参数下比所有伴随敏感性分析更有效率的方式。

总的来说，为了达成扩展性、最佳的、可维护的微分方程及神经网络整合框架， 可以切换不同的梯度方法，而不会改变其餘的代码，是一件极其重要的事。 而这正是 DiffEqFlux.jl 要带给使用者的。当中有三个相似的 API 函数：

然而，要把自动微分的反向模式层切换到前向模式层，只需要改变一个字符即可。 由於基于 Julia 的自动微分可以作用在 Julia 代码上， 原生的 Julia 微分方程求解器可以直接从这里受到助益。

结论

机器学习与微分方程注定是要在一起的，因为他们是在描述非线性世界的互补方法。 在 Julia 的生态中，我们以一种崭新而独立的套件整合了微分方程以及深度学习套件， 让这两个领域可以直接结合在一起。 由软件开启这样的可能性，目前仅仅是个开端。我们希望未来的博客文章可以混合两个领域， 在深度学习框架中能有更深入而酷炫的应用，像是整合我们即将上线的计量药物（pharmacometric）模拟引擎 Pumas.jl。 在全方位的微分方程求解器支援 ODEs、SDEs、DAEs、DDEs、PDEs、离散随机方程等多样微分方程式下， 我們期待你們將會用 Julia 建構怎樣的次世代的神經網路。

备注：可引用版本将在 Arxiv 上公开。