数组是任何编程语言的关键组成部分,特别是对于像 Julia 这样的面向数据的语言。数组根据其位置存储值:在 Julia 中,给定一个二维数组 A,表达式 A[1,3] 返回存储在称为 (1,3) 的位置的值。例如,如果 A 存储 Float64 数字,则此表达式返回的值将是一个 Float64 数字。
Julia 的数组通常从 1 开始对它们的轴进行编号,这意味着一维数组 a 的第一个元素是 a[1]。选择 1 与 0 似乎会引发一些讨论。Julia 环境中一个相当近期的添加是定义从任意索引开始的数组的能力。这篇博文的目的是描述为什么这可能很有趣。这确实是一篇“面向用户”的博文,暗示了此新功能如何简化您的生活的一些方法。对于希望编写支持具有任意索引的数组的代码的开发人员,请参阅此文档页面。
为什么我们应该关心数组具有哪些索引?第一个示例
有时数组用作简单的列表,在这种情况下,索引可能与您无关。但在其他情况下,数组用作连续量的离散表示(例如,在空间或时间上定义的值),在这种情况下,数组索引以可能具有意义的方式对应于“位置”。
作为一个简单的例子,考虑旋转图像的过程
| img | img_rotated |
|---|---|
 |  |
许多语言都提供用于旋转图像的函数;在 Julia 中,您可以使用 ImageTransformations 中定义的 warp 函数来执行此操作。
当您想要将旋转图像中的像素与原始图像中的像素进行比较时,事情会变得更加“有趣”。这些像素究竟是如何匹配的?换句话说,对于位置 img[i,j],img_rotated 中对应的 i′,j′ 位置是什么?在许多语言中,弄清楚这些类型的几何对齐可能不是一项简单的任务;毫不夸张地说,在复杂的情况下(例如,具有复杂空间变形的三维图像),人们可能要花费一整天甚至更多的时间来弄清楚两幅图像中的像素/体素应该如何进行比较。
为什么这是一个如此困难的问题?核心问题是,在大多数情况下,语言本质上是在对你“撒谎”关于像素的位置:如果数组始终沿任何给定轴从 1 开始索引,则数组索引并不真正对应于绝对空间位置。索引 1 表示“第一个索引”,而不是“空间位置 1”。
因此,为了在 Julia 中解决此问题,从 0.5 版本开始,我们支持索引不从 1 开始的数组。让我们通过指定我们希望上述旋转围绕摄像师头部的一个点进行来说明这一点。让我们加载图像
julia> using Images, TestImages
julia> img = testimage("cameraman");
julia> summary(img)
"512×512 Array{Gray{N0f8},2}"summary 显示 img 是一个灰度图像,索引范围为 1:512×1:512。使用任何几种方法(例如,ImageView 并注意状态栏以获取鼠标指针位置),我们可以了解到点 (y=126, x=251) 位于摄像师的头部。因此,让我们定义围绕此点的旋转
julia> using Rotations, CoordinateTransformations
julia> tfm = Translation(125,250) ∘ LinearMap(RotMatrix(pi/6)) ∘ Translation(-125,-250)
AffineMap([0.866025 -0.5; 0.5 0.866025], [141.747, -29.0064])这将 tfm 定义为平移(将头部移到原点)后跟旋转,然后再次平移的组合。(您可以通过键入 \circ 然后按 TAB 来获得组合运算符 ∘。)如果我们将此变换应用于图像,我们将得到一个有趣的结果
julia> img_rotated = warp(img, tfm);
julia> summary(img_rotated)
"-107:592×-160:539 OffsetArray{Gray{N0f8},2}"也许令人惊讶的是,img_rotated 的索引范围为 -107:592×-160:539,这意味着我们通过 img_rotated[-107,-160] 访问左上角,通过 img_rotated[592,539] 访问右下角。如果我们查看 img 的角是如何被 tfm 变换的,就不难看出这些数字是如何产生的
julia> using StaticArrays
julia> itfm = inv(tfm)
AffineMap([0.866025 0.5; -0.5 0.866025], [-108.253, 95.9936])
julia> itfm(SVector(1,1))
2-element SVector{2,Float64}:
-106.887
96.3597
julia> itfm(SVector(512,1))
2-element SVector{2,Float64}:
335.652
-159.14
julia> itfm(SVector(1,512))
2-element SVector{2,Float64}:
148.613
538.899
julia> itfm(SVector(512,512))
2-element SVector{2,Float64}:
591.152
283.399这表明输出的索引跨越变换坐标的区域。
输出保留坐标这一事实使得比较图像变得微不足道
julia> cv = colorview(RGB, paddedviews(0, img, img_rotated, img)...)paddedviews(0, arrays...) 使用 0 对输入数组进行填充(如果需要),以使它们都具有相同的索引,并且 colorview(RGB, r, g, b) 将灰度图像 r、g 和 b 分别插入到红色、绿色和蓝色通道中。如果我们可视化 cv,我们将看到以下内容
| 围绕图像中心 | 围绕头部 (cv) |
|---|---|
 |  |
左侧的图像是参考,显示了正确对齐时围绕图像中心的旋转会是什么样子。右侧的图像对应于上面采取的步骤,并且确实确认了旋转是围绕头部进行的。或者,我们可以像这样关注这些图像的重叠部分
julia> inds = map(intersect, indices(img), indices(img_rotated))
(1:512, 1:512)
julia> imgi = img[inds...];
julia> imgri = img_rotated[inds...];以便 colorview(RGB, imgi, imgri, imgi) 显示为

由于像素的索引编码了绝对空间位置,因此跟踪不同像素如何对齐变得微不足道:一个图像中的像素 i,j 对应于另一个图像中的像素 i,j。即使我们的坐标变换比简单的旋转复杂得多,情况也是如此。
在说明了为什么这可能有用之后,让我们退一步,更系统地了解一下数组索引。
具有任意索引的数组的系统介绍
在 Julia 中,如果我们定义一个数组
julia> A = collect(reshape(1:30, 5, 6))
5×6 Array{Int64,2}:
1 6 11 16 21 26
2 7 12 17 22 27
3 8 13 18 23 28
4 9 14 19 24 29
5 10 15 20 25 30然后我们可以像这样引用一个矩形区域
julia> B = A[1:3, 1:4]
3×4 Array{Int64,2}:
1 6 11 16
2 7 12 17
3 8 13 18对于某些应用程序,提取块的一个缺点是没有任何记录表明新块源自何处
julia> B2 = A[2:4, 1:4]
3×4 Array{Int64,2}:
2 7 12 17
3 8 13 18
4 9 14 19
julia> B2[1,1]
2因此,B2[1,1] 对应于 A[2,1],尽管事实上,根据它们的索引衡量,这些不是相同的位置。
为了保持我们索引的一致“命名”,让我们使用 OffsetArrays 包
julia> using OffsetArrays
julia> B3 = OffsetArray(A[2:4, 1:4], 2:4, 1:4)
# wrap the snipped-out piece in an OffsetArray
OffsetArrays.OffsetArray{Int64,2,Array{Int64,2}} with indices 2:4×1:4:
2 7 12 17
3 8 13 18
4 9 14 19
julia> B3[3,4]
18
julia> A[3,4]
18因此,B3 中的索引与 A 中的索引匹配。实际上,B3 甚至没有一个名为 (1,1) 的元素
julia> B3[1,1]
ERROR: BoundsError: attempt to access OffsetArrays.OffsetArray{Int64,2,Array{Int64,2}}
with indices 2:4×1:4 at index [1, 1]
Stacktrace:
[1] throw_boundserror(::OffsetArrays.OffsetArray{Int64,2,Array{Int64,2}}, ::Tuple{Int64,Int64}) at ./abstractarray.jl:426
[2] checkbounds at ./abstractarray.jl:355 [inlined]
[3] getindex(::OffsetArrays.OffsetArray{Int64,2,Array{Int64,2}}, ::Int64, ::Int64) at /home/tim/.julia/v0.6/OffsetArrays/src/OffsetArrays.jl:89在这种情况下,我们通过显式地将提取的数组“包装”在一个允许您提供自定义索引的类型中来创建 B3。(您可以使用 parent(B3) 检索刚刚提取的部分。)我们可以通过调整索引来做同样的事情
julia> using IdentityRanges
julia> ind1, ind2 = IdentityRange(2:4), IdentityRange(1:4)
(IdentityRange(2:4), IdentityRange(1:4))一个 IdentityRange 是一个索引与其值匹配的范围,r[i] == i。(ind1, ind2 = OffsetArray(2:4, 2:4), OffsetArray(1:4, 1:4) 在功能上将是等效的。)让我们使用 ind1 和 ind2 剪切数组的区域
julia> B4 = A[ind1, ind2]
OffsetArrays.OffsetArray{Int64,2,Array{Int64,2}} with indices 2:4×1:4:
2 7 12 17
3 8 13 18
4 9 14 19
julia> B4[3,4]
18这实现了简单的组合规则
如果 C = A[ind1, ind2],则 C[i, j] == A[ind1[i], ind2[j]]
因此,如果您的索引有自己的非常规索引,它们将被传播到下一阶段。
此技术也可用于创建“视图”
julia> V = view(A, ind1, ind2)
SubArray{Int64,2,Array{Int64,2},Tuple{IdentityRanges.IdentityRange{Int64},IdentityRanges.IdentityRange{Int64}},false} with indices 2:4×1:4:
2 7 12 17
3 8 13 18
4 9 14 19
julia> V[3,4]
18
julia> V[1,1]
ERROR: BoundsError: attempt to access SubArray{Int64,2,Array{Int64,2},Tuple{IdentityRanges.IdentityRange{Int64},IdentityRanges.IdentityRange{Int64}},false} with indices 2:4×1:4 at index [1, 1]
Stacktrace:
[1] throw_boundserror(::SubArray{Int64,2,Array{Int64,2},Tuple{IdentityRanges.IdentityRange{Int64},IdentityRanges.IdentityRange{Int64}},false}, ::Tuple{Int64,Int64}) at ./abstractarray.jl:426
[2] checkbounds at ./abstractarray.jl:355 [inlined]
[3] getindex(::SubArray{Int64,2,Array{Int64,2},Tuple{IdentityRanges.IdentityRange{Int64},IdentityRanges.IdentityRange{Int64}},false}, ::Int64, ::Int64) at ./subarray.jl:184请注意,此对象是一个常规 SubArray(它不是 OffsetArray),但因为它传递了 IdentityRange 索引,所以它保留了索引的索引。
第二个应用程序:数组/图像过滤(卷积)
如上所述的图像旋转示例,Images 包的最近版本 (v0.6.0) 将处理具有自定义索引的数组的功能和责任都交给了用户。此包中的一个关键函数是 imfilter,它可以用于平滑或以其他方式“过滤”数组。其思想是从数组 A 开始,每个局部邻域都由“内核”kern 加权,根据以下公式生成输出值
让我们从一个简单的例子开始:让我们使用“狄拉克 delta 函数”内核进行过滤,这意味着它在位置 0 处的值为 1,在其他任何地方都为零。根据相关公式,因为 kern[J] 在 J==0 处为 1,所以这应该只是给我们一个原始数组的副本
julia> using Images
julia> imfilter(1:8, [1])
WARNING: assuming that the origin is at the center of the kernel;
to avoid this warning, call `centered(kernel)` or use an OffsetArray
Stacktrace:
[1] depwarn(::String, ::Symbol) at ./deprecated.jl:64
[2] _kernelshift at /home/tim/.julia/v0.6/ImageFiltering/src/imfilter.jl:1049 [inlined]
[3] kernelshift at /home/tim/.julia/v0.6/ImageFiltering/src/imfilter.jl:1046 [inlined]
[4] factorkernel(::Array{Int64,1}) at /home/tim/.julia/v0.6/ImageFiltering/src/imfilter.jl:1016
[5] imfilter at /home/tim/.julia/v0.6/ImageFiltering/src/imfilter.jl:10 [inlined]
[6] imfilter(::UnitRange{Int64}, ::Array{Int64,1}) at /home/tim/.julia/v0.6/ImageFiltering/src/imfilter.jl:5
[7] eval(::Module, ::Any) at ./boot.jl:235
[8] eval_user_input(::Any, ::Base.REPL.REPLBackend) at ./REPL.jl:66
[9] macro expansion at ./REPL.jl:97 [inlined]
[10] (::Base.REPL.##1#2{Base.REPL.REPLBackend})() at ./event.jl:73
while loading no file, in expression starting on line 0
8-element Array{Int64,1}:
1
2
3
4
5
6
7
8警告告诉您,Images 决定对您的意图进行猜测,即内核 [1] 意在围绕零居中。您可以通过显式传递以下内核来抑制警告
julia> kern = centered([1])
OffsetArrays.OffsetArray{Int64,1,Array{Int64,1}} with indices 0:0:
1
julia> kern[0]
1
julia> kern[1]
ERROR: BoundsError: attempt to access OffsetArrays.OffsetArray{Int64,1,Array{Int64,1}} with indices 0:0 at index [1]
Stacktrace:
[1] throw_boundserror(::OffsetArrays.OffsetArray{Int64,1,Array{Int64,1}}, ::Tuple{Int64}) at ./abstractarray.jl:426
[2] checkbounds at ./abstractarray.jl:355 [inlined]
[3] getindex(::OffsetArrays.OffsetArray{Int64,1,Array{Int64,1}}, ::Int64) at /home/tim/.julia/v0.6/OffsetArrays/src/OffsetArrays.jl:94通过使用 OffsetArray,您已清楚地指定了 kern 的预期索引。
这可以用来以下列方式移动图像(默认情况下,imfilter 在与输入相同的域上返回其结果)
julia> kern2 = OffsetArray([1], 2:2) # a delta function centered at 2
OffsetArrays.OffsetArray{Int64,1,Array{Int64,1}} with indices 2:2:
1
julia> imfilter(1:8, kern2, Fill(0)) # pad the edges of the input with 0
8-element Array{Int64,1}:
3
4
5
6
7
8
0
0
julia> kern3 = OffsetArray([1], -5:-5) # a delta function centered at -5
OffsetArrays.OffsetArray{Int64,1,Array{Int64,1}} with indices -5:-5:
1
julia> imfilter(1:8, kern3, Fill(0))
8-element Array{Int64,1}:
0
0
0
0
0
1
2
3这些都在下图中进行了说明
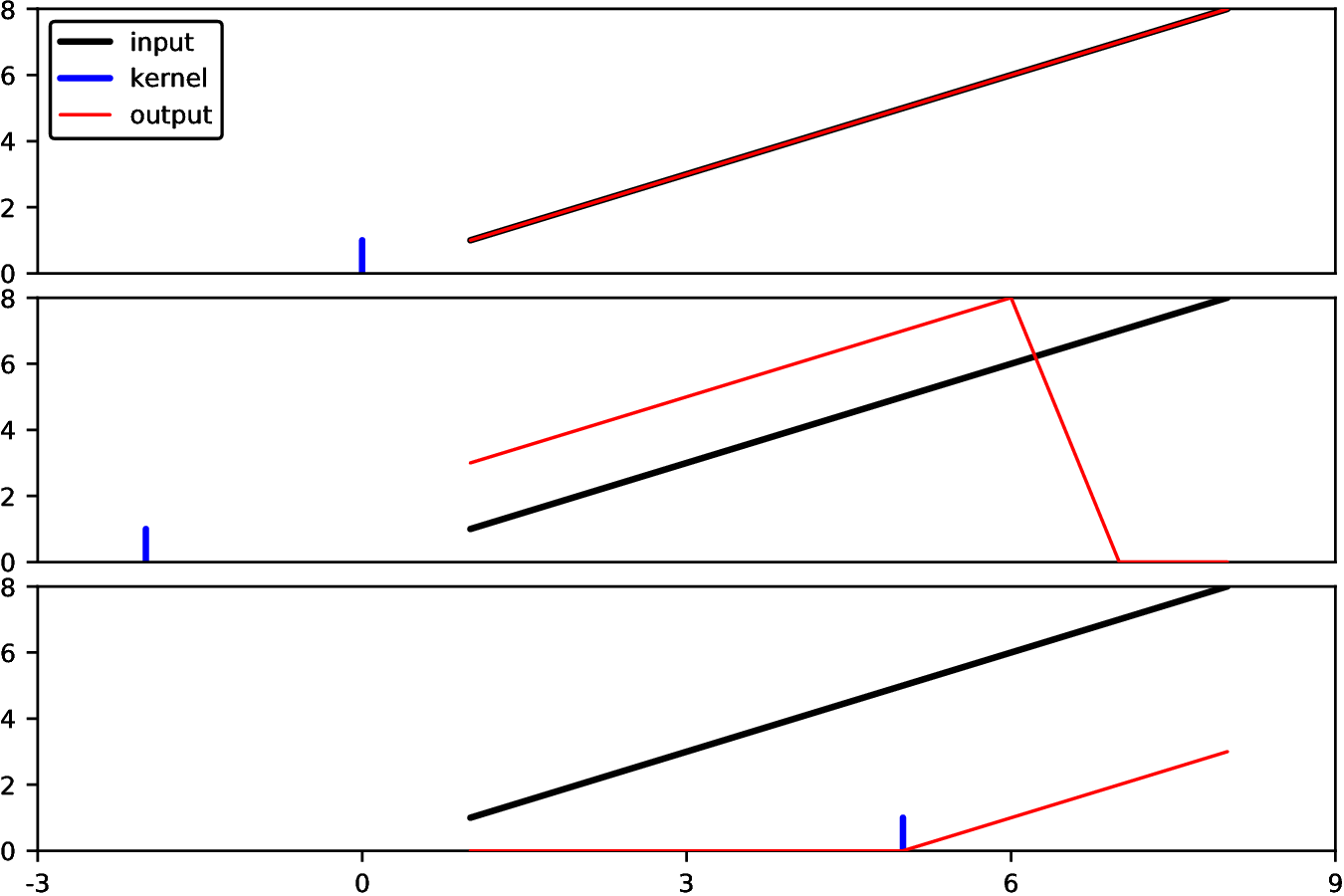
在此图中,我们将内核绘制为位于对应于卷积而不是相关的的位置。
在其他编程语言中,当使用具有偶数个元素的内核进行过滤时,可能很难记住两个中间元素中的哪一个对应于原点。在 Julia 中,这不是问题,因为您可以自己做出选择
julia> kern = OffsetArray([0.5,0.5], 0:1)
OffsetArrays.OffsetArray{Float64,1,Array{Float64,1}} with indices 0:1:
0.5
0.5
julia> imfilter(1:8, kern, Fill(0))
8-element Array{Float64,1}:
1.5
2.5
3.5
4.5
5.5
6.5
7.5
4.0
julia> kern = OffsetArray([0.5,0.5], -1:0)
OffsetArrays.OffsetArray{Float64,1,Array{Float64,1}} with indices -1:0:
0.5
0.5
julia> imfilter(1:8, kern, Fill(0))
8-element Array{Float64,1}:
0.5
1.5
2.5
3.5
4.5
5.5
6.5
7.5同样地,有时我们的应用程序可能无法正确处理边缘,并且我们希望将其丢弃。例如,考虑以下二次函数
julia> a = [(i-3)^2 for i = 1:9] # a quadratic function
9-element Array{Int64,1}:
4
1
0
1
4
9
16
25
36
julia> imfilter(a, Kernel.Laplacian((true,)))
9-element Array{Int64,1}:
-3
2
2
2
2
2
2
2
-11边缘上的那些奇怪的值(没有填充可以“外推”二次函数)可能会导致问题。因此,让我们只提取定义良好的值,这意味着相关公式的所有输入都具有显式分配的值
julia> imfilter(a, Kernel.Laplacian((true,)), Inner())
OffsetArrays.OffsetArray{Int64,1,Array{Int64,1}} with indices 2:8:
2
2
2
2
2
2
2请注意,在这种情况下,它返回了一个OffsetArray,以便结果中的值与原始数组正确对齐。
最后一个应用:傅里叶变换
您可以使用自定义索引做更多的事情。作为最后一个示例,考虑一下离散傅里叶变换,它是在周期域上定义的。通常,用数组模拟周期域相当困难,因为数组的大小是有限的。但是,可以定义具有周期行为的索引对象。这里我们使用FFTViews包,在一个简单的正弦波上演示该技术
julia> using FFTViews
julia> a = [sin(2π*x)+0.1 for x in linspace(0,1,16)];
julia> afft = FFTView(fft(a))
FFTViews.FFTView{Complex{Float64},1,Array{Complex{Float64},1}} with indices FFTViews.URange(0,15):
1.6+0.0im
1.498-7.53098im
-0.288537+0.69659im
-0.236488+0.35393im
-0.222614+0.222614im
-0.216932+0.14495im
-0.214217+0.0887316im
-0.212937+0.0423558im
-0.212557+0.0im
-0.212937-0.0423558im
-0.214217-0.0887316im
-0.216932-0.14495im
-0.222614-0.222614im
-0.236488-0.35393im
-0.288537-0.69659im
1.498+7.53098im现在,正如每个学习傅里叶变换的学生都知道的那样,0 频率 bin 包含a中值的总和
julia> afft[0]
1.6000000000000003 + 0.0im由于正弦波的平均值为零,因此(在舍入误差范围内)为 16 * 0.1 = 1.6。
我们还可以检查傅里叶峰处的幅度,并探索结果的周期性
julia> afft[1]
1.4980046017247872 - 7.53097769363728im
julia> afft[-1] # negative frequencies are OK
1.4980046017247872 + 7.53097769363728im
julia> afft[64+1] # look Ma, it's periodic!
1.4980046017247872 - 7.53097769363728im
julia> length(indices(afft,1)) # but we still know how big it is
16鉴于afft的周期性,常用的fftshift函数(例如,fftshift(fft(a)))可以用afft[-8:7]替换。虽然非常简单,但这些技术使得处理有时可能变得复杂且容易出错的索引体操变得令人惊讶地更加愉快。
总结:用户的视角
这仅仅触及了自定义索引可能实现的皮毛。在作者看来,它们的主要优势在于,它们可以通过确保“名称”(索引)可以赋予绝对含义来提高代码的清晰度,而不是总是“参考此特定数组的第一个元素恰好编码的内容”。
有相当多的代码尚未正确考虑自定义索引的可能性——当然,其中一些是由本文作者编写的!因此,用户应该准备好应对利用自定义索引会在基础 Julia 或包中触发错误的可能性。用户不要放弃,鼓励他们将此类错误报告为问题,因为这是自定义索引随着时间的推移获得可靠支持的唯一途径。
总结:开发人员的视角
对于某些算法,似乎几乎没有理由在除了 1 基索引之外的任何内容上使用数组;在这种情况下,可能没有理由修改现有代码。但是,如果您的代码具有“空间”解释——位置有意义——那么您可能想尝试一下新功能。
在转换现有代码时,本文作者观察到以下趋势
利用自定义索引的算法有时比其“1 锁定”对应算法更容易理解;
如果您要移植旧代码以支持自定义索引,则有一些坏消息:如果您在第一次编写代码时必须仔细考虑索引,那么即使最终结果稍微简单一些,通常也需要大量投资才能重新考虑索引。
即使特定算法从支持任意索引中获得的优势可能很小,从一开始就编写“索引感知”代码通常并不比编写隐式假设索引从 1 开始的算法更难。
开发人员请参阅Julia 的文档以获取更多指导。